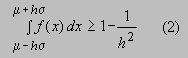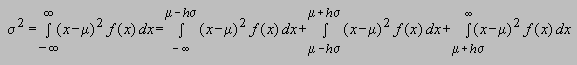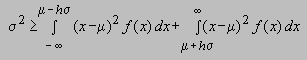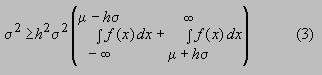| Pafnutiy Lvovich Chebyshev. Nació el 4 de mayo de 1821 en la aldea rusa de Okatovo. A los 16 años se matriculó en la Facultad de Física y Matemáticas de la Universidad de Moscú y acabó la carrera en 1841. Murió el 26 de noviembre de 1894. Es uno de los creadores e integrantes de la escuela de matemática de Petersburgo. Su fama entre los estudiantes de las matemáticas se debe a la famosa desigualdad que lleva su nombre, y que pasaremos a estudiar a continuación. |
|
Supongamos que tenemos una determinada función de distribución F, y supongamos además que esta función de distribución tiene asociada una función de densidad (aunque no es estrictamente necesaria esta condición), es decir probaremos la desigualdad de Chebyshev para el caso especial en que la ley de probabilidad es continua con función de densidad f.
La desigualdad de Chebyshev establece que si tenemos una ley de probabilidad con media finita m y varianza finita s2, entonces
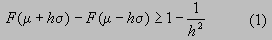
Definamos la cantidad Q(h) por
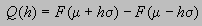
La expresión (1), al introducir la función de densidad, se puede denotar por
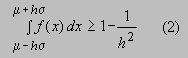
Para demostrar (2) recordemos la definición de la varianza, esto es
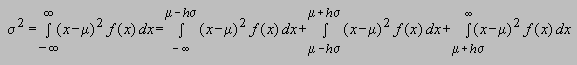
de modo que se obtiene la siguiente desigualdad
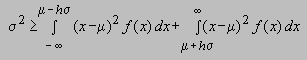
Ahora bien, en el caso de la primera integral, la estamos efectuando en el dominio de x < m - hs, y en este caso se cumple la desigualdad (x - m)2 > h2s2 . De manera similar, la segunda integral la estamos efectuando en el dominio x > m+- hs, y en este caso también se cumple la desigualdad (x - m)2 > h2s2. De modo que si sustituimos la cantidad (x - m)2 por estas cotas inferiores en ambas integrales, obtenemos que
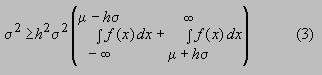
Podemos observar que la suma de las dos integrales en (3) es simplemente 1 - Q(h). De modo que hemos demostrado que
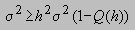
es decir,
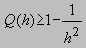
Que es exactamente la expresión (1).
Los resultados de esta desigualdad son sorprendentes, y muestran con mayor vehemencia el papel que juega la dispersión s. En efecto, supongamos que tenemos una variable aleatoria X con media y varianza finita, entonces la expresión (1) es equivalente a
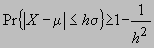
Y esta expresión indica que hay una probabilidad superior al 75% de que un valor observado de X caiga dentro de dos desviaciones estándar de la media. Para esto basta hacer h = 2. De manera análoga, con probabilidad superior al 15/16 = 0.9375 un valor observado de X caerá dentro de cuatro desviaciones estándar de la media, para esto basta hacer h = 4.
