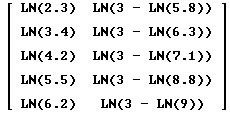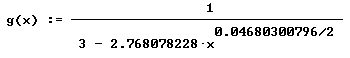Tercera actividad

Objetivos de esta actividad: El alumno deberá se capaz de encontrar la recta en mínimos cuadrados que se ajustan a una nube de datos bidimensionales, así como debe discernir si tal ajuste es correcto basando su decisión en el coeficiente de Pearson y en el error de estimación estándar. Además el alumno deberá ser capaz de ajustar cualquier modelo "linealizable" a un conjunto de datos bidimensionales, y saber calcular el error estándar de estimación, y poder discernir en base al criterio del menor error estándar de estimación para determinar cual es el mejor modelo ajustado a estos datos bidimensionales.

Actividades

 Se han observado los pares (X, Y), obteniéndose los siguientes resultados: 

X

2.3

3.4

4.2

5.5

6.2

Y

5.8

6.3

7.1

8.8

9.0

 Considere los siguientes tres modelos: 

Y = a + bX

Y = exp(3 + aX -3b)

  Y = 1 / (3 + bX- (a / 2) )

Obtenga los estimadores mínimo cuadráticos de  a y b para cada uno de los tres modelos

Para realizar este ejercicio haga lo siguiente:
1. Abra el programa DERIVE
2. En la opción Editar - Matriz, entregue las dimensiones de Filas = 5 y Columnas = 2, ingrese los datos de manera que en la primera columna estén las X y el la segunda columna las Y
3. A la matriz construida asígnele la letra M, mediante la instrucción M : = "oprima la tecla F3" (cuidando que el video reverso esté marcando la matriz construida", F3 en el DERIVE es un "copy")
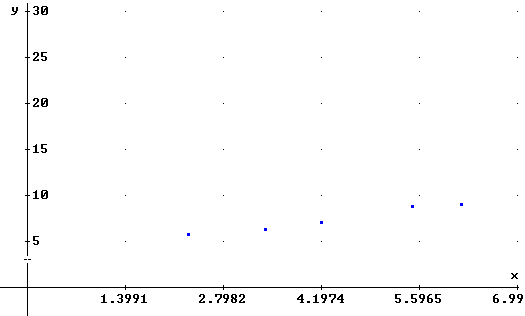
4. Grafique la "nube de puntos" en la opción gráfica del DERIVE, para esto haga click en el icono , entrará a una nueva ventana donde estará el plano cartesiano, entonces oprima Insertar, cuidando que en video reverso de la primera ventana esté en la matriz.. Deberá aparecer algo similar a

5. Vuelva a la ventana inicial oprimiendo el icono que está en el extremo superior derecho de la ventana gráfica.
6. Ahora usted ajustará una recta a estos puntos, mediante la técnica de mínimos cuadrados. Para esto en el editor escriba lo siguiente FIT ([x, a + bx], M). Sea riguroso con los paréntesis. Oprima la tecla Enter. Luego posicione el video reverso en la expresión resultante y oprima el icono . Deberá aparecer la expresión

0.9059586542·x + 3.486258613

que es la "mejor recta en mínimos cuadrados" que se ajusta a los datos.
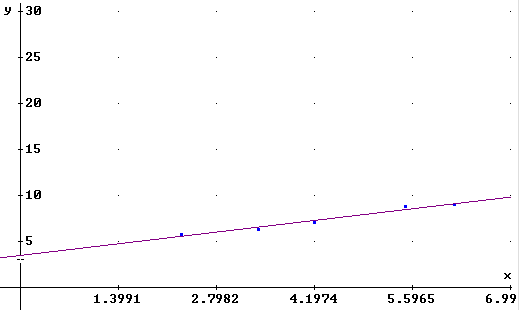
7. Ahora asegurándose que el video reverso marque este último resultado vuelva a la pantalla gráfica y grafique esta última expresión. Deberá aparecer lo siguiente

8. Ejecute en el editor lo siguiente f(x) : = 0.9059586542·x + 3.486258613
9. Ahora trabajará con el segundo modelo, y lo que tenemos que hacer es llevarla a una forma lineal. Aplinado logaritmo natural nos queda la expresión Ln (Y) = 3 + a X -3b. Luego hacemos el arreglo  - a X - 3b = 3 - Ln(Y), a la cual nuevamente le aplicamos logaritmo natural, esto es Ln(-a) - 3b Ln(X) = Ln( 3 - Ln(Y) ). De manera que nos queda una recta en las variables Ln(X), como variable independiente, y Ln(3 - Ln(Y) ) como variable dependiente. 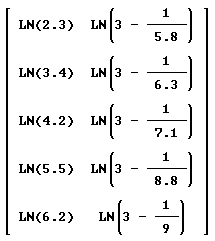Entonces debemos formar una nueva matriz de datos con estos valores para cada X y cada Y de los datos antiguos. La matriz resultante deberá lucir de la siguiente manera:

10. A esta matriz defínala por H : = F3 (cuidando que el video reverso esté ubicada en esta nueva matriz). Observe que en esta matriz la columna le puede asignar por la letra Z, y la segunda columna por la letra W, de modo que tenemos el modelo lineal W = c + d Z, donde c = Ln (-a) y d = -3b. De esta forma toda vez que estimemos la recta W = c + d Z, podemos estimar los valores de a y b del modelo original.
11. En el editor escriba FIT([ z, c + dz], H), luego Enter. Enseguida calcule esta expresión mediante haciendo click en el signo de aproximación. Deberá resultar lo siguiente

0.6691337780 - 0.4776350091·z
12. Para calcular el valor de a del modelo original escriba la siguiente expresión en el editor: ln(-a) = 0.6691337780
13. Asegurándose que el video reverso este en esta última expresión vaya al menú Resolver eligiendo el submenú Expresión, acepte lo que aparecerá en la caja de diálogo. Obtendrá el resultado a = -1.952545250
14. Para calcular el valor de b del modelo original escriba la siguiente expresión en el editor: -3b = - 0.4776350091. De manera similar resuelva esta ecuación y obtendrá b = 0.1592116697.
15. Escriba con estos valores calculado la expresión del modelo, esto es

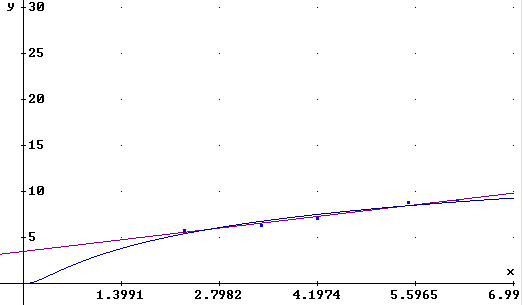
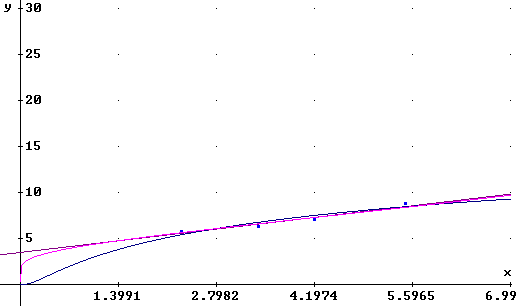
16. Defina la expresión por h(x) : = F3 (cuidando que el video reverso se encuentre en esta última expresión). Luego vaya a la ventana gráfica y grafique esta última expresión de la manera habitual. Deberá aparecer lo siguiente:

17. Realice una construcción análoga para estimar los parámetros del último modelo. Con la matriz transformada de datos

El modelo ajustado debería ser
18. Grafique este último modelo de la forma habitual.

Cuestionario
1. ¿Cuál es el valor del error de estimación estándar para cada uno de los modelos?
2. ¿Cuál es el mejor modelo?
3. Calcule el coeficiente lineal de Pearson para cada una de las matrices construidas