|
Sobre medias y varianzas de subpoblaciones |
||
|
Media total Hemos aprendido que para un conjunto de datos, digamos
los principales parámetros para el análisis descriptivo estadístico son la media y la varianza, esto es
Ahora supongamos que los datos dados en (1) están particionados en k clases, y donde cada clase tiene ni elementos, con i = 1, .., k. Es decir los datos en (1) son equivalentes a
donde en primer subíndice indica la clase a la cual pertenece la observación, y el segundo subíndice indica la posición dentro de la clase, y además obviamente (puesto que son los mismos datos):
Realizando el cálculo, nuevamente, para esta nueva notación de los cálculos, según la expresión (2), tenemos que
Y esta última expresión se puede escribir en función de las medias de cada clase. En efecto,
puesto que para cada i fijo se tiene que
La expresión del extremo derecho de (3) es lo que se conoce como media total, en el sentido que es la simple media que todos conocemos pero que ahora está en función de las medias de cada clase. |
Varianza total Un desarrollo similar podemos utilizar para calcular la varianza muestral para los datos según la notación dada en (2). En efecto, la varianza muestral conforme a esta notación será:
Para nada es complicado verificar que,
Por otro lado, se sabe que la varianza para cada clase i es,
de manera que despejando la suma cuadrática en esta última expresión, tenemos que
y la reemplazamos en (4), nos queda
Ahora si en esta última expresión reemplazamos la media por la fórmula de la media total tenemos
Y la expresión (5) es la que se conoce como varianza muestral total, y su única efectividad es que está calculada en términos de las medias y varianzas de cada clase.
|
|
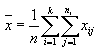
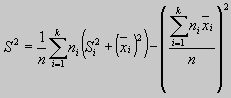 (5)
(5)