Análisis Factorial

Contenido

• Introducción
• Modelo Matemático del Análisis Factorial
• ¿Cuándo es adecuado realizar un AF?
• Fases del Análisis Factorial
• 1. Extracción de Factores Comunes
• 2. Rotación de Factores
• 3. Cálculo de las Puntuaciones factoriales

Introducción

El análisis factorial (AF) es una técnica de análisis multivariante que se utiliza para el estudio e interpretación de las correlaciones entre un grupo de variables. Parte de la idea de que dichas correlaciones no son aleatorias sino que se deben a la existencia de factores comunes entre ellas. El objetivo del AF es la identificación y cuantificación de dichos factores comunes.

Por ejemplo, hay fenómenos como estilo de vida, imagen de un producto, actitudes de compra, nivel socioeconómico, que es necesario conocer pero que no se pueden medir con una sola pregunta, porque se trata de fenómenos complejos que se manifiestan en infinidad de situaciones, sentimientos, comportamientos y opiniones concretas. Estos fenómenos son el resultado de la medición de un conjunto de características. El AF nos permitirá combinar preguntas de manera que podamos obtener nuevas variables o factores que no son directamente medibles pero que tienen un significado.

Se trata de una técnica adecuada para el caso de variables continuas altamente correlacionadas.

Modelo Matemático del Análisis Factorial

El modelo matemático del AF supone que cada una de las p variables observadas es función de un número m factores comunes (m < p) más un factor específico o único. Tanto los factores comunes como los específicos no son observables y su determinación e interpretación es el resultado del AF.

Analíticamente, supondremos un total de p variables observables tipificadas y la existencia de m factores comunes. El modelo se define de la siguiente forma:

X₁ = l₁₁ F₁ + l₁₂ F₂ + l_1m F_m + e₁
X₂ = l₂₁ F₁ + l₂₂ F₂ + l_2m F_m + e₂
...
X_p = l_p1 F₁ + l_p2 F₂ + l_pm F_m + e_p

que podemos expresar de forma matricial como:  X = Lf + e

donde:

• X es el vector de las variables originales.
• L es la matriz factorial. Recoge las cargas factoriales ó (saturaciones).
• l_ih es la correlación entre la variable j y el factor h.
• f es el vector de factores comunes.
• e es el vector de factores únicos.

Como tanto los factores comunes como los específicos son variables hipotéticas, supondremos, para simplificar el problema, que:

1. Los factores comunes son variables con media cero y varianza 1. Además se suponen incorrelacionados entre sí.
2. Los factores únicos son variables con media cero. Sus varianzas pueden ser distintas. Se supone que están incorrelacionados entre sí. De lo contrario la información contenida en ellos estaría en los factores comunes.
3. Los factores comunes y los factores únicos están incorrelacionados entre si Esta hipótesis nos permite realizar inferencias que permitan distinguir entre los factores comunes y los específicos.

Basándonos en el modelo y en las hipótesis formuladas, podemos demostrar que la varianza (información contenida en una variable) de cada variable se puede descomponer en:

• aquella parte de la variabilidad que viene explicada por una serie de factores comunes con el resto de variables que llamaremos comunalidad de la variable
• y la parte de la variabilidad que es propia a cada variable y que, por tanto, es no común con el resto de variables. A esta parte se le llama factor único o especificidad de la variable.

Var(x_j ) = 1 = l ²_j1 Var(F₁ ) + l ²_j2 Var(F₂ ) + ... + l ²_jm Var(F_m ) + Var(e_j ) = l ²_j1 + l ²_j2 + l ²_jm + Var(e_j )

donde:

• l ²_jh representa la proporción de varianza total de la variable X_j explicada por el factor h.
• h ²_j = l ²_j1 + l ²_j2 + ... + l ²_jm es la comunalidad de la variable X_j y representa la proporción de varianza que los distintos factores en su conjunto explican de la variable X_j. Es, por tanto, la parcela de esa variable que entra en contacto con el resto de variables. Varía entre 0 (los factores no explican nada de la variable) y 1 (los factores explican el 100% de la variable).
• Var(e_j ) es lo que llamamos especificidad y representa la contribución del factor único a la variabilidad total de X_j.
• l ²_1h + l ²_2h + ... + l ²_ph = g_h es lo que se llama eigenvalue (autovalor) y representa la capacidad del factor h para explicar la varianza total de las variables. Si las variables originales estuviesen tipificadas, la varianza total sería igual a p y g_h/p representaría el porcentaje de varianza total atribuible al factor h.

El objetivo del AF será, por tanto, obtener los factores comunes de modo que expliquen una buena parte de la variabilidad total de las variables.

¿Cuándo es adecuado realizar un AF?

Un AF resultará adecuado cuando existan altas correlaciones entre las variables, que es cuando podemos suponer que se explican por factores comunes. El análisis de la matriz de correlaciones será pues el primer paso a dar. Analíticamente, podemos comprobar el grado de correlación con las siguientes pruebas o test:

• Test de esfericidad de Bartlett.
  

  Es necesario suponer la normalidad de las variables. Contrasta la H₀ de que la matriz de correlaciones es una matriz identidad (incorrelación lineal entre las variables). Si, como resultado del contraste, no pudiésemos rechazar esta H₀, y el tamaño de la muestra fuese razonablemente grande, deberíamos reconsiderar la realización de un AF, ya que las variables no están correlacionadas.

  El estadístico de contraste del test de Bartlett es:

  B = - ( n - 1 - (2p + 5)/6 ) ln | R^* |
  bajo la hipótesis nula resulta  X ²_{(p2 - p)/2}

  donde:

  • p es el número de variables y
  • | R^* | es el determinante de la matriz de correlaciones muestrales.
• Indice KMO (Kaiser-Meyer-Olkin) de adecuación de la muestra.
  

  KMO se calcula como:

  

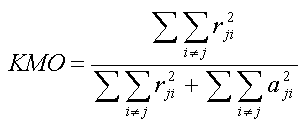
  donde:

  • r_ji - coeficiente de correlación observada entre las variables j e i.
  • a_ji - coeficiente de correlación parcial entre las variables j e i.

  Estos coeficientes miden la correlación existente entre las variables j e i, una vez eliminada la influencia que las restantes variables ejercen sobre ellas. Estos efectos pueden interpretarse como los efectos correspondientes a los factores comunes, y por tanto, al eliminarlos, a_ji - representará la correlación entre los factores únicos de las dos variables, que teóricamente tendría que ser nula. Si hubiese correlación entre las variables (en cuyo caso resultaría apropiado un AF), estos coeficientes deberían estar próximos a 0, lo que arrojaría un KMO próximo a 1. Por el contrario, valores del KMO próximos a 0 desaconsejarían el AF.

  Está comúnmente aceptado que:

  • Si KMO < 0.5 no resultaría aceptable para hacer un AF.
  • Si 0.5 < KMO < 0.6 grado de correlación medio, y habría aceptación media.
  • Si KMO > 0.7 indica alta correlación y, por tanto, conveniencia de AF.
• Medida de adecuación de la muestra para cada variable (MSA)
  

  Este índice es similar al KMO, pero para cada variable. La j-ésima variable de MSA viene dada por la siguiente expresión:

  

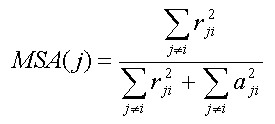
  Si el valor del MSA fuera pequeño, no se aconsejaría el AF. Por el contrario, valores próximos a 1 indicarían que la variable X_j es adecuada para incluirla con el resto en un AF. En muchas ocasiones, se eliminan las variables con MSA muy bajo. (diagonal principal de la matriz de correlación anti-imagen).

• Correlación anti-imagen AIC.
  

  El coeficiente de correlación antiimagen es el negativo del coeficiente de correlación parcial entre dos variables. Si existiesen factores comunes, esperaríamos pequeños coeficientes de correlación parcial. Por ello, el AF es aplicable cuando en la matriz de correlaciones antiimagen hay muchos coeficientes pequeños.

Fases del Análisis Factorial

1. Extracción de los factores comunes.
2. Rotación de los factores con objeto de facilitar su interpretación.
3. Puntuaciones factoriales.

1. Extracción de Factores Comunes

Existen distintos métodos de estimación de los coeficientes de la matriz factorial L: los más comunes (para un AF exploratorio) son el método de las Componentes Principales y el método de Ejes Factoriales.

Para proceder a la estimación de los coeficientes factoriales vamos a partir de la identidad fundamental del AF proporcionada por Thurstone en 1.947:

R = LL' + w

donde:

• R  es la matriz de correlaciones entre las variables.
• w  es la matriz de varianzas y covarianzas de los factores únicos.

Consideramos una transformación de R: R - w = LL' = R^* (matriz de correlación reducida) cuyos elementos diagonales son las comunalidades y el resto, los coeficientes de correlación lineal entre las variables originales. La idea consiste en determinar L partiendo de alguna estimación para R^*, y a partir de ella calcular los coeficientes de la matriz L. Podemos optar por dos métodos:

Método 1 - AF de Componentes Principales (ACP)

El método de componentes principales se basa en suponer que los factores comunes explican el comportamiento de las variables originales en su totalidad de manera que el modelo es:

X = Lf

Las comunalidades iniciales de cada variable son igual a 1, porque el 100% de la variabilidad de las p variables se explicará por los p factores. Evidentemente, carecería de interés sustituir las p variables originales por p factores que, en ocasiones, son de difícil interpretación. No obstante, si las correlaciones entre las p variables fuesen muy altas, sería de esperar que unos pocos factores explicasen gran parte de la variabilidad total. Supongamos que decidimos seleccionar r factores. La comunalidad final de cada variable indicará la proporción de variabilidad total que explican los r factores finalmente seleccionados.

La estimación de los coeficientes l _j se obtiene diagonalizando la matriz de correlaciones.

Método 2 - AF de Ejes Factoriales (PAF)

En este método partimos de la base de que sólo una parte de la variabilidad total de cada variable depende de factores comunes y, por tanto, la comunalidad inicial no será 1. Estima dichas comunalidades mediante los coeficientes de determinación múltiple de cada variable con el resto. Se sustituyen estos valores en la diagonal principal de la matriz R^* y se procede a efectuar un ACP. Una vez obtenido el resultado, se estiman de nuevo las comunalidades, se vuelven a sustituir en la diagonal principal de la matriz R^* y el proceso se retroalimenta hasta alcanzar un criterio de parada (por ejemplo cuando la diferencia entre lasa comunalidades de dos iteraciones sucesivas sea menor que una cantidad prefijada).

La elección de uno u otro método (ACP o PAF) depende de los objetivos del AF. Así el ACP es adecuado cuando el objetivo es resumir la mayoría de la información original (varianza total) con una cantidad mínima de factores con propósitos de predicción. El AFC resulta adecuado para identificar los factores subyacentes o las dimensiones que reflejan qué tienen en común las variables. El inconveniente del método PAF es que el cálculo de las comunalidades requiere mucho tiempo y muchos recursos informáticos y, además, no siempre se pueden estimar o, incluso, pueden ser no válidas (comunalidades menores que 0 o mayores que 1).

Empíricamente, se llega a resultados muy parecidos cuando el número de variables excede de 30 o las varianzas compartidas exceden de 0.6 para la mayoría de las variables.

2. Rotación de Factores

La interpretación de los resultados del AF se basará en el análisis de las correlaciones entre las variables y los factores que como sabemos viene dado por las cargas factoriales.

Para que dicha interpretación sea factible, es recomendable que:

• Las cargas factoriales de un factor con las variables estén cerca de 0 ó de 1. Así, las variables con cargas próximas a 1 se explican en gran parte por el factor, mientras que las que tengan cargas próximas a 0 no se explican por el factor.
• Una variable debe tener cargas factoriales elevadas con un sólo factor. Es deseable que la mayor parte de la variabilidad de una variable sea explicada por un solo factor.
• No debe haber factores con similares cargas factoriales

Así, si con la solución inicial no se consiguiese una fácil interpretación de los factores, éstos pueden ser rotados de manera que cada una de las variables tenga una correlación lo más próxima a 1 con un factor y a 0 con el resto de factores. Como hay menos factores que variables, conseguiremos que cada factor tenga altas correlaciones con un grupo de variables y baja con el resto. Si examinásemos las características de las variables de un grupo asociado a un factor, se podrían encontrar rasgos comunes que permitan identificar el factor y darle una denominación que responda a esos rasgos comunes. Así, conseguiremos desvelar la naturaleza de las interrelaciones existentes entre las variables originales. Los tipos de rotaciones más habituales son la ortogonal y la oblicua.

La rotación ortogonal permite rotar los factores estimados inicialmente, de manera que se mantenga la incorrelación entre los mismos. El método más utilizado de rotación es la varimax (Varianza máxima), ideado por Kaiser. La rotación oblícua no mantiene la ortogonalidad de los factores, lo que nos lleva a aceptar que dos o más factores expliquen a la vez una misma realidad. Las comunalidades finales de cada variable permanecen inalteradas con la rotación.

3. Cálculo de las Puntuaciones factoriales

Una vez estimados los factores comunes, es importante calcular las puntuaciones de los sujetos (individuos u objetos) investigados para saber cuánto puntúan en cada factor. Así, podremos:

• Sustituir los valores de las p variables originales para cada sujeto de la muestra por las puntuaciones factoriales obtenidas. En la medida en que el número de factores es menor que el número de variables iniciales, si el porcentaje de explicación de la varianza total fuese elevado, dichas puntuaciones factoriales podrían sustituir a las variables originales en muchos problemas de análisis o predicción. Además, muchas técnicas estadísticas se ven seriamente afectadas por la correlación entre las variables originales. En la medida en que las puntuaciones factoriales estén incorrelacionadas podrán utilizarse en ulteriores análisis.
• Colocar a cada sujeto en una determinada posición en el espacio factorial y conocer qué sujetos son los más raros o extremos, dónde se ubican ciertos grupos de la muestra, los más jóvenes frente a los mayores; los de clase alta frente a los de clase media o baja; los creyentes frente a los no creyentes, etcétera,  obteniendo en qué factores sobresalen unos y otros.