Podemos observar la figura 1. En ella se establecen las variables características de un sistema dinámico.

Figura 1

En efecto, el recipiente que está conteniendo el fluido representa a la variable de estado del sistema, es ella y solo ella que indica el estado de la situación del sistema, si nuestro interés en el sistema es saber el volumen o nivel del liquido acumulado en el estanque. Los grifos de entrada y salida son las variables de flujo, y en este caso son ellas y solo ellas que hacen que la variable es estado evolucione a través del tiempo, incluso si hay equilibrio, es decir el volumen o el nivel permanecen constante es porque el flujo de salida y el de entrada tienen el mismo valor (aceptando el hecho trivial que ambos grifos estén cerrados).

Decíamos que este recipiente está conteniendo agua, si observamos este sistema como un sistema hidrodinámico simple. Un oficinista, un economista y un matemático tendrían diferentes apreciaciones sobre este mismo modelo. Un oficinista va a identificar el estanque como el trabajo que le queda por hacer en su escritorio, donde la variable de flujo de entrada es las tareas que le entregan diariamente, y la variable de flujo de salida es el trabajo diario que realiza. Un economista, al observar la cantidad contenida en el estanque posiblemente lo identificará con la deuda que mantiene su organización empresarial, donde el flujo de entrada es el déficit anual que hace incrementar su deuda acumulada, y bel flujo de salida es el pago anual de una cantidad para poder disminuir la deuda . Un matemático puede ver una suerte de integral, en efecto, si denota por al volumen del estanque en el tiempo t, entonces tendrá que

donde y son los flujos de entrada y salida, respectivamente. La interpretación del matemático da pauta para establecer que la unidad de tiempo puede ser de tipo continua, esto es fracciones de años, o mese o días, o milésimas de segundo.

Siguiendo con estas ideas, supongamos ahora el símil hidrodonámico de la figura 1 más sencillo todavía. Vamos a suponer que no tiene un grifo de salida, es decir la situación quedaría como la indica la figura 2.

Figura 2

En este caso el estanque solo está acumulando. Con este modelo vamos a acudir al punto de vista de un estadístico. Lo más probable que lo identifique con una suerte de frecuencia, en que el grifo se abre para avisar que un determinado resultado que nos interesa ha sido contabilizado y pasa a engrosar una unidad más de la frecuencia de ese resultado. La figura 2 se puede volver dibujar como,

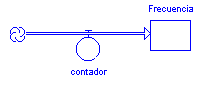
Figura 3

Donde el grifo de entrada lo hemos renombrado como "contador" y la variable de estado se llama ahora "frecuencia". La pregunta ahora es ¿quién abre el grifo?. Veamos un ejemplo concreto, supongamos que se lazará 20 veces una moneda insesgada al aire y se contará el número de caras. De modo que la variable de estado "frecuencia" contabilizará en número de veces que obtengamos cara, y esta información será detectada por "contador". Muy bien, la persona que lanzará 20 veces la moneda lo hará de una manera muy especial, puesto que la moneda es insesgada, este lanzamiento es equivalente a sacar aleatoriamente un número entre 0 y 1, de tal manera que si el número es menor que 0.5 consideraremos haber obtenido una "cara", en caso contrario es "sello". De manera que tendremos una nueva variable, que será la encargada de "lanzar la moneda" veinte veces. Definamos esta variable como "lanzador" (de monedas) y toda vez que lance una moneda conforme sea el resultado le avisará a la variable de flujo "contador" donde ella discernirá si es cara o sello. La situación se puede esquematizar en la figura 4,

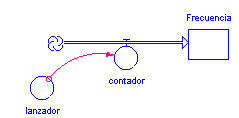
Figura 4

La flecha que va desde el lanzador al contador significa la información que envía la variable lanzador a la variable de flujo contador. La variable lanzador simplemente la definimos internamente como "elige un número entre 0 y 1", que por lo general en cualquier lenguaje de programación se escribe como RANDOM (0,1). Mediante la flecha o "conector" que envía a la contador, este se programará de la siguiente forma: "si el número que me envía lanzador es menor que 0.5 entonces contabilizo una cara, si por el contrario (es mayor que 0.5) nada contabilizo porque resultó sello". Entonces a contador se le programa de la siguiente manera: IF LANZADOR < 0.5 THEN 1 ELSE 0. Finalmente le indicamos a este programa que efectué 20 lanzamientos. Notemos que la variable de estado "frecuencia" no ejecuta ninguna instrucción, ella simplemente recibe lo que le envía contador, solo debe señalar que ella está en el valor "cero" en el inicio, es decir no lleva ninguna ventaja o valor inicial. En definitiva nuestro sistema dinámico programado queda como:

Vamos a explicar el código de programación. La variable frecuencia acompañada con el icono está expresando que va a sumar al valor frecuencia que ya tiene en la iteración anterior (t – dt) el nuevo valor que asumirá la variable de flujo contador, cuya fórmula es la definida, como lo establecimos anteriormente, al lado del icono . Finalmente la variable lanzador, a continuación del icono , se define con la expresión random (0,1).

Ahora bien, ya establecido el modelo dinámico que determinará la frecuencia de obtención de "caras" en el lanzamiento de 20 veces una moneda, vamos a indicarle a nuestro programa que el "tiempo" (dt) es discreto, de uno en uno, y que además la longitud del tiempo corresponde a 20 lanzamientos. Para esto hacemos simplemente dt=1 y detenemos el programa en el tiempo = 20. Esto es

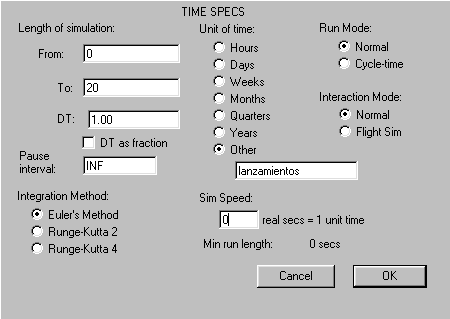
Nota: A estas alturas es conveniente decir que estamos utilizando el software STELLA 5.1.1

Hacemos correr esta simulación y, en nuestro caso, obtenemos los siguientes resultados, indicado en la tabla 1. Lo que en definitiva hemos realizado es una simulación del lanzamiento de una moneda 20 veces y donde además hemos contado el número de caras, es decir la frecuencia de "caras" en los 20 lanzamientos.

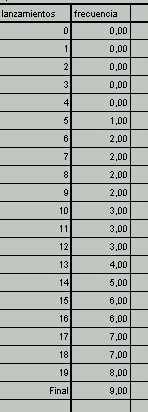
Tabla 1

Volver a la página principal