Teoría de juegos: donkey games

Eliseo Martínez

Es común en ciertos juegos de ocio donde se “avanza” conforme a los resultados de un dado, como por ejemplo el ludo (parchís, en España) se castiga al jugador que obtiene tres “6” seguidos (se regresa a “casa”). En efecto, obtener un seis en el ludo es un buen resultado, pues se avanza seis casillas, y además permite repetir el lanzamiento, de modo que si se obtiene otro seis, entonces se está en mejor situación, puesto que no solo avanza otras seis casillas más sino que además repite un tercer lanzamiento... Ahora viene el peligro: si saca otro seis de vuelta a casa. Surge entonces la pregunta ¿Le gustaría jugar con un dado que está “levemente” cargado a obtener el número seis?

Suponiendo que tenemos un dado que está sesgado hacía el seis más que otro número, y además uno solo de los jugadores del ludo puede jugar con este dado trucado. En un primer razonamiento pareciera que con este dado el jugador tiene más posibilidades de ganar, sin embargo vamos a ver que con estas altas probabilidades de ganar las ganancias del jugador van a disminuir, de ahí el nombre de “donkey games” o “juegos de burro”.

Vamos a estudiar un sencillo juego tipo donkey, que fue analizado por Juan M. R. Parrondo, en la sección Juegos Matemáticos, en la revista Investigación y Ciencia de abril del 2002. El juego consiste en lo siguiente: se tiene una moneda que tiene asignada la probabilidad p de obtener “cara” y probabilidad 1-p de obtener “sello” (cruz, en España). Si el jugador lanza la moneda y obtiene “cara” entonces gana un euro (utilizo el mismo tipo de moneda, €, que aparece en el mencionado artículo, y de paso rindo un homenaje al tratado comercial entre Chile y la Unión Europea, firmado un día antes en que se preparan estos apuntes de divulgación), si sale “sello” pierde un euro. Pero si al lanzar nuevamente la moneda sale el mismo resultado anterior, entonces se cancela la ganancia o pérdida anterior. Nos explicamos. Supongamos que se obtiene la siguiente evolución del jugador: “sello-cara-cara-cara-sello-sello”, entonces su ganancia ha sido de -2. En efecto, con el primer sello se pierde un euro, con la segunda cara se gana un euro (en total cero ganancia), con la tercera cara se pierde lo ganado anteriormente (queda con –1 euro), con la cuarta cara gana un euro (cero ganancias, entonces), con el sello en el quinto lanzamiento pierde un euro, pero al obtener un sello en el sexto lanzamiento se cancela la pérdida anterior, es decir obtiene un euro. En total un euro de ganancia.

Desde el punto de vista de la teoría de juegos (o la teoría de la decisión) podemos configurar este juego de una forma estructural no sin hacer antes la siguiente observación: es fundamental la tener en mente la jugada anterior, puesto que se gana o se pierde conforme se obtiene el mismo resultado “dos veces seguidas”, pero en el entendido que toda vez que ocurra dos veces seguida el mismo resultado, empieza una nueva contabilidad, de manera que en rigor, el propio jugador está jugando con su pasado inmediatamente anterior, y lo que puede haber ocurrido en la jugada anterior es o haber obtenido una “cara”, o haber obtenido un “sello” o no tener ninguna contabilidad puesto que fue en la jugada anterior que se repitió una jugada y que en el turno presente se “empieza a jugar de nuevo”. Con esta aclaración entonces podemos definir dos jugadores. El primer jugador es el que lanza la moneda, de manera que sus acciones o jugadas son “cara” o “sello”, y el segundo jugador será una pizarra en que se anota lo que aconteció en la jugada anterior, y hay tres posibles resultados, en la pizarra no hay nada anotado (“ninguno”,que denotaremos por N), que significa que en ese momento se repitió un resultado anterior, o que está anotado una “cara” (C), o está anotado un “sello” (S). En resumen, las jugadas del primer jugador son {cara, sello} (C y S, respectivamente), y las jugadas de la pizarra son {ninguno, cara, sello} (N, C y S, respectivamente). La matriz de pagos o ganancia para cada jugador es como sigue:

		Valor anotado	antes de lanzar
		Ninguno	Cara	Sello
Resultado	Cara	(+1,Cara)	(-1,Ninguno)	(+1,Cara)
de la tirada	Sello	(-1,Sello)	(-1,Ninguno)	(+1,Ninguno)

Tabla1

Donde la primera ordenada muestra lo que gana o pierde el jugador que lanza la moneda, y la segunda ordenada corresponde al nuevo valor que toma la pizarra.

Definamos como el valor obtenido por la pizarra al cabo del n-ésimo lanzamiento, de manera que , y definamos por el valor obtenido en la moneda en el n-ésimo lanzamiento, de modo que . Es claro que para cualquier n las variables aleatorias son independientes esto es el resultado de lo que se obtendrá en el lanzamiento n+1 nada tiene que ver con el historial que describe la (pizarra) variable . Con esto es fácil concluir lo siguiente:

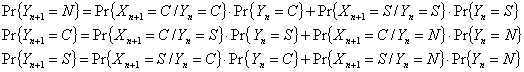
en virtud de la independencia entre se tiene que,

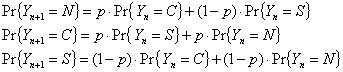
Matricialmente las ecuaciones anteriores se pueden expresar como:

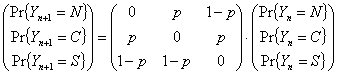
Ahora bien, la matriz de Markov que regula este proceso tiene claramente las condiciones para que exista la distribución asintótica, y esta se obtiene resolviendo el sistema

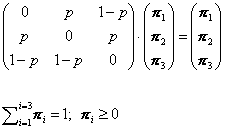
La solución de este sistema es

Vamos a calcular ahora la ganancia esperada del primer jugador. Observando la tabla 1 podemos observar que el jugador ganará un euro o perderá un euro conforme a lo que esté anotado en la pizarra. Esto es, si en la pizarra está anotado “sello”, entonces cualquiera que sea el resultado de la moneda ganará un euro; si en la pizarra está anotado “cara” entonces cualquiera sea el resultado de la moneda perderá un euro; ahora si en la pizarra está anotado “ninguno” entonces la ganancia o pérdida de un euro dependerá del resultado de la moneda (cara con probabilidad p, sello con probabilidad 1-p). Por otro lado la distribución asintótica para que en la pizarra aparezca “ninguno”, “cara” o “sello” están dadas por los valores de , respectivamente. En definitiva, la ganancia esperada del jugador que lanza la moneda es

La gráfica de la ganancia en función de p se entrega a continuación,

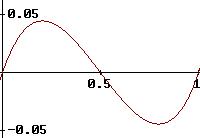
Para esta función ganancia el máximo se obtiene cuando p = 0.203820, y la mínima ganancia se obtiene en p = 0.796179. De manera que es más conveniente jugar, este “juego tonto”, con una moneda que nos “desfavorezca” (en la obtención de “cara”).

Modelación dinámica de este juego

No es muy trivial la modelación de este juego en STELLA. Existe un pequeño inconveniente en la programación de la “pizarra”. La programación de una moneda con probabilidad p de obtener cara y 1-p de obtener sello es en extremo sencilla, sin embargo la dificultad radica en encontrar un modo de anotar los resultados de una secuencia de caras y sellos en la pizarra de manera que toda vez que aparezcan dos resultados iguales se anote “ninguno”, veamos un ejemplo. Supongamos que una trayectoria posible es 2 1 1 2 2 1 2 1 2 2 1 1 2 1 1 1, (1 es cara y 2 es sello) , entonces en la “pizarra” deberá aparecer la siguiente secuencia notacional 2 1 0 2 0 1 2 1 2 0 1 0 2 1 0 1, donde 1 significa cara, 2 sello, y 0 es “ninguno”. Observemos la figura 1.

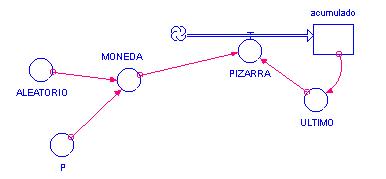
Figura 1

Este diagrama de Forrester representa la simulación del lanzamiento de la moneda y la notación en la pizarra conforme a la tabla 1. La variable MONEDA simula el resultado de lanzar una moneda, la variable de flujo PIZARRA es la que anota conforme los resultados de la segunda componente de la tabla 1 y lo realiza de la siguiente manera: la variable ULTIMO describe el último resultado anotado en la variable de estado “acumulado”, luego la variable PIZARRA anotará el resultado observando lo que “ya” está anotado en la pizarra (entregado por la variable ULTIMO) y por el resultado “actual” obtenido en MONEDA.

Las ecuaciones dinámicas para el diagrama de la figura 1 son:

acumulado(t+dt) = acumulado(t) + PIZARRA * dt

acumulado inicial = 0

PIZARRA = IF MONEDA = ULTIMO THEN 0 ELSE MONEDA

ULTIMO = acumulado – DELAY(acumulado,dt,0)

ALEATORIO = RANDOM (0,1)

MONEDA = IF ALEATORIO < P THEN 1 ELSE 2

P = 1/4

Ahora para determinar las probabilidades o frecuencias asintóticas, al realizar un gran número de simulaciones completamos el programa con el siguiente diagrama indicado en la figura 2,

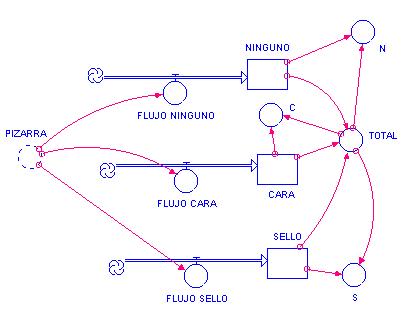
Figura 2

Las ecuaciones dinámicas de la programación completa se entrega a continuación

acumulado(t) = acumulado(t - dt) + (PIZARRA) * dt

INIT acumulado = 0

PIZARRA = IF MONEDA=ULTIMO THEN 0 ELSE MONEDA

CARA(t) = CARA(t - dt) + (FLUJO_CARA) * dt

INIT CARA = 0

FLUJO_CARA = IF PIZARRA=1 THEN 1 ELSE 0

NINGUNO(t) = NINGUNO(t - dt) + (FLUJO_NINGUNO) * dt

INIT NINGUNO = 0

FLUJO_NINGUNO = IF PIZARRA= 0 THEN 1 ELSE 0

SELLO(t) = SELLO(t - dt) + (FLUJO_SELLO) * dt

INIT SELLO = 0

FLUJO_SELLO = IF PIZARRA=2 THEN 1 ELSE 0

ALEATORIO = random(0,1)

C = CARA/TOTAL

MONEDA = if ALEATORIO < P then 1 else 2

N = NINGUNO/TOTAL

P = 1/4

S = SELLO/TOTAL

TOTAL = NINGUNO+CARA+SELLO

ULTIMO = acumulado-DELAY(acumulado,DT,0)

Si realizamos una pasada de 5000 iteraciones obtenemos los siguientes resultados para las frecuencias N (ninguno), C (cara) y S (sello), indicados en la tabla 2:

Tabla 2

Resultados que “casi” coinciden (como era de esperar) con las probabilidades asintóticas indicadas en (1) al hacer p = ¼. En rigor = 0.371428 , = 0.2 y = 0.428571, respectivamente.