Robert Brown, con toda seguridad, no fue el primero en descubrir el movimiento que lleva su nombre. A consecuencia de sus viajes se fue interesando en la investigación de los coloides, y en la cuidadosa observación de preparaciones microscópicas en el estudio de los mecanismos de reproducción en las plantas. Sin embargo, el comportamiento errático del polen suspendido en una solución lo asoció a las teorías vitalistas de la vida, haciendo defensa de que este movimiento era propio de la materia viviente, y relacionado con los mecanismos de la reproducción. Sin embargo, en sus trabajos finales concluye que el movimiento errático observado era de naturaleza mecánica y no dependía del carácter orgánico ni inorgánico de los objetos microscópicos observados. Esto ocurría en el año 1828.

Parecía claro la no existencia de un modelo matemático para este movimiento: la Matemática y la Física del siglo XIX no estaban lo suficientemente desarrolladas para atacar el fenómeno. Fue necesario esperar los trabajos de Einstein, en 1905, para su modelación. Y la barrera fundamental que impedía el conocimiento del movimiento Browniano era justamente el determinismo clásico de la Mecánica de Newton. Esta aseguraba que todo movimiento debía tener por causa una fuerza. Einstein usando la teoría molecular cinética de la materia prueba que dicho movimiento se produce sin que medie la acción de fuerza externa alguna. Su razonamiento es de una sencillez extrema: si los granos de polen en suspensión se mueven es porque las moléculas del líquido chocan con ellos. las moléculas a su vez están en movimiento constante por efecto de fuerzas externas al líquido (interacciones moleculares o, incluso, por cambios producidos en los niveles de energía en la estructura subatómica). De este modo Einstein llegó a la conclusión de que el movimiento Browniano es intrínseco a la materia.

Supongamos que denota la trayectoria de una partícula que está sometida a choques con moléculas (por ejemplo, dentro de un fluido); el desplazamiento de esta partícula, en un intervalo de tiempo de longitud se mide mediante , luego este desplazamiento, aparte de deberse a la velocidad de la partícula en ese momento, se agregará otro que puede ser proporcional a un desplazamiento, debido a interacciones azarosas, denotado por . Supongamos que y que la velocidad en el tiempo y en la posición , es , se tendrá entonces que

(1)

 siendo el factor de proporción que eventualmente puede depender del tiempo y la posición . Digamos que el desplazamiento se explica por una parte determinística, el primer término de la suma en el lado derecho de (1), y por una parte aleatoria, indicada por el segundo término del lado derecho de (1). De manera más general,

(2)

 Observemos que si obedece las leyes de alguna probabilidad, se tendrá que, en definitiva, , y por ende , será una variable aleatoria.

Ahora bien, si es una variable aleatoria, entonces una posible trayectoria, conforme a la ley de probabilidad que la rige, se denotará por , donde es el resultado obtenido del espacio de probabilidad en que se sustenta la variable . Salvo cuando sea absolutamente necesario la trayectoria de la denotaremos simplemente por .

 3. El movimiento Browniano unidimensional y su modelación.

 Supongamos que es una colección de variables aleatorias, diremos que este proceso es un movimiento Browniano si tiene las siguientes propiedades:

 (i) para es una variable aleatoria normalmente distribuida con media 0 y varianza .

 (ii) para , es un conjunto de variables aleatorias independientes.

 Recordemos que una variable aleatoria se distribuye con media y varianza (que denotaremos por ) si la ley de probabilidad es

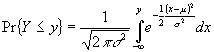(3)

de manera que la propiedad (i) nos dice que para

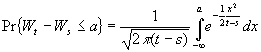(4)

 y la propiedad (ii) nos dice que para se tiene que

 La aparente complejidad de estas propiedades matemáticas son realmente sencillas de interpretar (o modelar).

Sea , intentaremos crear una posible trayectoria para cada valor de , esto es . Supongamos que por hipótesis , ¿cómo se obtiene ?, para esto acudimos a la variable aleatoria , donde sabemos que un posible valor para este incremento sigue una distribución normal , luego generamos un valor aleatorio según esta distribución y así obtenemos un valor para . Para generar el valor de , acudimos al incremento (observemos que ya sabemos el valor de , digamos ) que es obtenido mediante la generación de un número aleatorio según una distribución , sea este número , esto es , de modo que , y así continuamos con el proceso. De modo que para generar una posible trayectoria de este movimiento Browniano, se generan en forma independientes (garantizado por la propiedad (ii)) los incrementos , y se calcula la trayectoria mediante

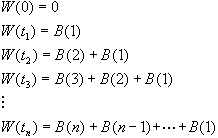
 sin olvidar que cada se ha obtenido de una distribución , cálculos que en general son más sencillo en cuanto es común establecer que la diferencia entre los tiempos () sea constante, esto es , de modo que se genera mediante una distribución .

 4. Aplicaciones del movimiento Browniano

En la sección 2 describíamos el movimiento de una partícula suspendida en un fluido, y que estaba influenciado por dos fuerzas. La primera, correspondía a un movimiento no aleatorio (determinístico) generado por la naturaleza subyacente del flujo del fluido o inducida por alguna fuerza externa impuesta sobre el sistema. La segunda, colisiones y/o relaciones de interacciones con otras partículas originan movimientos aleatorios que actúan en tiempos de corta duración, y que a menudo se describen correctamente por las fluctuaciones de un movimiento Browniano.. De manera que, para un periodo de tiempo desde hasta , el desplazamiento de la partícula se puede aproximar por

(5)

 donde es la localización de la partícula en el tiempo . Aquí es la velocidad instantánea del fluido en el tiempo y en la posición mientras que el cambio incremental asociado a un movimiento Browniano, , está representado por , y mide la varianza instantánea asociadas con las colisiones del proceso .

Ahora bien, la ecuación (5) se puede escribir en notación de diferenciales, esto es

(6)

 y esta es una ecuación diferencial estocástica. Si obviáramos la palabra "estocástica", que se debe a la diferencial , estaríamos tentado a integrar en el sentido clásico de Riemann-Stieltjes, para obtener alguna "solución" para , esto es

(7)

 sin embargo la segunda integral, que diremos integral estocástica, no puede recibir el tratamiento clásico, toda vez que el proceso Browniano no es de "variación acotada". Entonces la integral estocástica deberá tener un tratamiento especial. Existen dos versiones para el tratamiento de esta integral, digamos entonces que hay dos tipos de integrales estocásticas: la integral de Ito, y la integral de Stratonovich.

De momento nuestro interés será la identificación de algún fenómeno real que se pueda modelar según la ecuación (6).

Si bien es cierto que la ecuación (6) se obtuvo teniendo en cuenta consideraciones de la Física, veremos como el precio de las acciones se comportan como partículas que sufren fluctuaciones aleatorias debidos a interacciones. De paso, entregaremos un ejemplo de como un proceso discreto se puede aproximar a un proceso de difusión (en espera de la definición formal de un proceso de difusión, digamos que el de la ecuación (6) es un proceso de difusión, en virtud de las buenas propiedades del movimiento Browniano ).

Sea el precio de una determinada acción observada al término del ésimo día. Es común definir el retorno del precio de esta acción como

(8)

 Observemos que este retorno corresponde al incremento del día ésimo (positivo o negativo) respecto del precio de la acción del día anterior (en tanto por 1). Vamos a presentar un modelo que se puede catalogar de ingenuo, pero sin lugar a dudas nos ayudará a clarificar conceptos del Cálculo Estocástico. Supongamos que la sucesión admite la siguiente estructura

(9)

 donde es el retorno esperado y las variables son independientes y se distribuyen según una normal ; de manera tal que las son independientes e identicamente distribuidas según . Reemplazando (8) en (9),

 donde son i.i.d. según , de manera que

(10)

 Observemos que esta ecuación en diferencias finitas actúa en el espacio de tiempo discreto . Extendamos nuestro espacio de tiempo a , y efectuemos una partición, siempre discreta, de manera de proponer un modelo levemente más general, y que en cualquier caso cuando la partición coincida con el conjunto nos resulte la ecuación (10). Para , hagamos

(11)

 donde es un movimiento Browniano.

Si la partición es tal que su desplazamiento es constante, esto es , entonces si la ecuación (11) es en esencia la ecuación (10). Se puede demostrar, mediante técnicas avanzadas del Cálculo Estocástico, que toda vez que esta partición sea más fina, es decir cuando , entonces el proceso definido por la ecuación (11) converge (en distribución) a un proceso de difusión , que satisface la ecuación diferencial estocástica

(12)

 Observemos que la ecuación (12) es una caso particular de la ecuación (6). De manera que para obtener una trayectoria de la evolución del precio de la acción, , significa resolver la integración estocástica de .

Ahora bien, con estos antecedentes, estamos en condiciones de modelar el proceso entregado en (11) mediante la técnica de la Dinámica de Sistemas a través del software STELLA.

Modelo general con aplicación de Black and Sholes (B. Camacho y R. Letelier)

Volver al menú principal