Considere los siguientes vectores A= 12 i + j -12 k y B = 8 i + 4 j + k. Le sugerimos que los cálculos los realice en el DERIVE, escriba A : = [12, 1, -12] y B : = [8, 4, 1]; el producto punto se calcula como A . B, el producto cruz por CROSS(A, B); y la magnitud de A como ABS(A).
Responda lo siguiente.

1. La magnitud del producto A x B es

   1.   ?    15665
   2.   ?    125,1598977
   3.   ?    No se puede calcular
   4.   ?    135,5

2. El producto 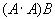es

   1.   ?    0
   2.   ?    1156
   3.   ?    2312 i + 1156 j + 280 k
   4.   ?    [2312, 1156, 289]

3. El producto 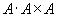es

   1.   ?    0 i + 0 j + 0 k, el vector nulo
   2.   ?    No está definido dicho producto
   3.   ?    0
   4.   ?    Es ambigua la expresión, tiene más de un resultado.

4. El coseno del angulo entre los vectores A y B es

   1.   ?    0.6754322346
   2.   ?    0.5568567345
   3.   ?    0.5751633986
   4.   ?    0

5. La expresión 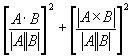es igual a

   1.   ?    1/2
   2.   ?    0
   3.   ?    2
   4.   ?    1

6. El seno del ángulo comprendido entre A y B vale

   1.   ?    0.5568567345
   2.   ?    0.8180385472
   3.   ?    0.789654674
   4.   ?    0.55

7. El ángulo comprendido entre A y B vale

   1.   ?    0.9579924482 radianes
   2.   ?    59.80817449 grados
   3.   ?    59.80817449 radianes
   4.   ?    0.9579924482 grados

8. El área del paralelogramo generado por los vectores A y B vale

   1.   ?    72.57994886
   2.   ?    52.57994886
   3.   ?    62.57994886
   4.   ?    42.57994886

9. El volumen del paralelepípedo formado por los vectores A, B y A x B es

   1.   ?    0
   2.   ?    imposible, no se puede formar
   3.   ?    1
   4.   ?    15665

10. El valor de A x (B x A) es

    1.   ?    [0, 0, 0]
    2.   ?    [1256, 1068, 1345]
    3.   ?    0
    4.   ?    no se puede realizar tal producto