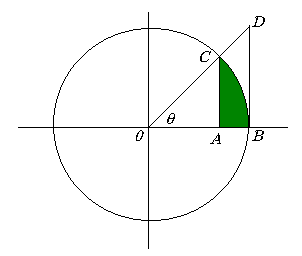
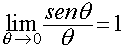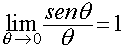| Consideremos el circulo unitario, esto es de radio 1, y
observemos la siguiente figura |
|
|
| Antes que nada debemos convencernos que el área del
sector circular indicada por los puntos OBC es igual a la
fracción q/2p del área del círculo
unitario que es p, esto es |
|
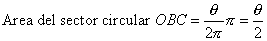
|
| Por otro lado es claro que área del triángulo OAC
< área del sector circular OBC < área del triángulo OBD.
|
| Además área del triángulo OAC = 1/2 cos q
sen q; y el área del triángulo OBD =
(1/2) (sen q / cos q).
De modo que tenemos la siguiente desigualdad |
|
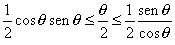
|
| multiplicando por la cantidad positiva (estamos en el
primer cuadrante) 2/sen q, nos queda |
|
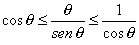
|
| Hacemos tender q hacia cero y
obtenemos que |
|
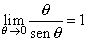
|
| y en consecuencia |
|
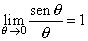
|