| En realidad algunos matemáticos llaman ecuación logística a la ecuación diferencial |
|
|
| y no a su solución, que ahora llamaremos función logística, que como sabemos es |
|
|
| Vamos a estudiar dos situaciones que son interesantes. La primera tiene que ver con la ecuación diferencial dada en (1); y la segunda con las posibles trayectorias de la solución dada en (2). |
| Diagrama de fase |
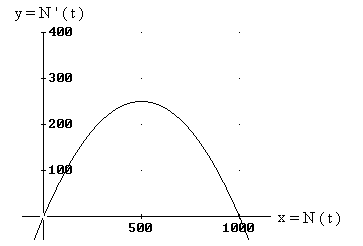
| La ecuación en (1) establece que la derivada N ' ( t ) está en función de N ( t ), de modo que podemos graficar a la derivada en función de N ( t ) y no de la variable tiempo. Para entender esto basta hacer y = N ' ( t ) con x = N ( t ), y nos queda la parábola |
|
y = (a - b x) x |
| cuya gráfica es (para a = 1 y b = 0.001) |
|
|
| De esta gráfica, llamada diagrama o plano de fase, se obtiene que en la raíz no nula, esto es en x = 1000 = a / b se consigue el llamado factor de carga. Y por otro lado el máximo de la parábola ocurre cuando N ( t ) = 500 que viene a marcar el punto de inflexión, puesto que allí se tiene que la pendiente de la recta tangente a la gráfica en ese punto, es y ' = N '' ( t ) = 0. De tal manera que, aún sin resolver la ecuación diferencial en (1), el diagrama de fase nos entrega las buenas propiedades que debe tener la función N ( t ). |
| Trayectorias de la función logística N ( t ). |
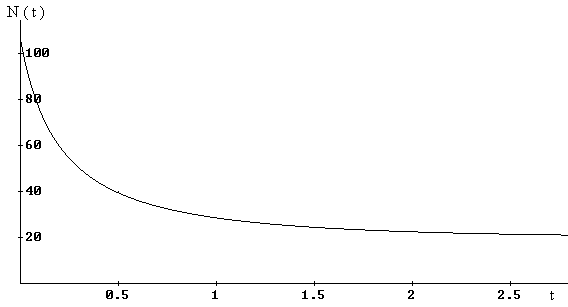
| En la sección de la ecuación logística presentábamos la gráfica de N ( t ), para a = 1 y b = 0.001. Sin embargo no siempre tiene la forma sigma (sigmoide). En efecto, hagamos un cambio de parámetros, a =1 y b = 0.05, y obtendremos una caída de la población que se estabilizará en a / b = 20 |
|
|
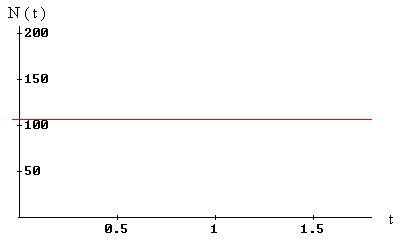
| Finalmente hagamos el siguiente cambio, a = 1 y b = (106) -1 = 0.009433962264; y obtenemos la gráfica siguiente donde simplemente la población permanece constante, |
|
|
| Note que en cualquiera de los tres casos la población se estabiliza en a / b. |
| Podemos probar experimentalmente que se obtendrá la gráfica sigmoide si N ( 0 ) < a / b. Se obtendrá la gráfica de "decaimiento" si N ( 0 ) > a / b. Y finalmente la evolución de N ( t ) será constante si N ( 0 ) = a / b |