Integrales de funciones par e impar

Recordemos que una función f( x ) es par en el intervalo [a, -a] si f( x ) = f( -x ). El ejemplo más trivial es f( x ) = x2 en el intervalo [-a, a], cualquiera sea el valor de a.
Y una función f( x ) será impar en el intervalo [a, b] si f( x ) = - f( -x ). Un ejemplo trivial es f( x ) = x3.
Las siguientes gráficas describen ambos tipos de funciones
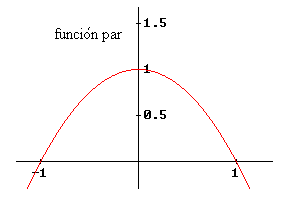
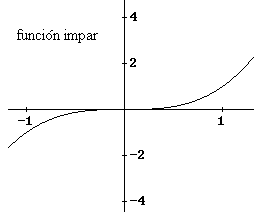
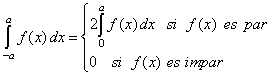Observando atentamente estas gráficas y manteniendo el concepto de la integral como área, es fácil convencerse que

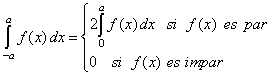
La más famosa de todas las funciones pares es la llamada densidad gaussiana, estas es

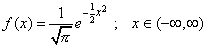
y cuya gráfica es

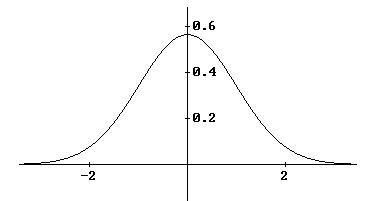
No resulta complicado verificar con el software DERIVE que

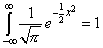
de modo que

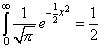
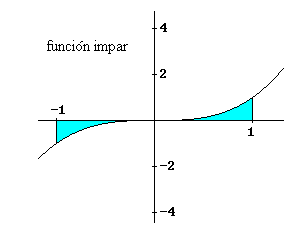
Finalmente, para la gráfica de la función impar, f( x ) = x3, que se entrega a continuación es claro que la integral entre [-1, 1] es cero, puesto que es la suma de un área positiva y un área negativa con el mismo valor absoluto,