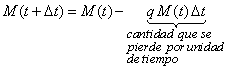| Aceptemos lo siguiente: la razón de decaimiento de un
material radioactivo es proporcional a la cantidad presente. |
| Esto significa que si M( t ) es la cantidad
de masa (por ejemplo gramos) del material radioactivo, entonces la
cantidad de masa radioactiva en el tiempo t + Dt
se rige por la ecuación dinámica siguiente, |
|
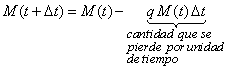
|
| Formando el cociente de Newton y pasando al límite
cuando Dt se aproxima a cero, nos
queda |
|
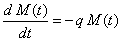
|
| la solución general de esta ecuación diferencial es |
|

|
| Ahora si suponemos que la cantidad inicial de material
radioactivo, en t = 0, es M0 podemos concluir
que M( 0 ) = M0 y en consecuencia el modelo de
decaimiento de la sustancia radioactiva nos queda como |
|
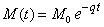
|
| Esta ecuación es extremadamente útil para la detección
de la antigüedad de ciertos fósiles (creo que de casi todos los
fósiles a través de la desintegración del llamado carbono 14 que los
animales tenemos, incluido nosotros) |
| La vida media de una sustancia radiactiva
se define como el tiempo necesario para que se desintegre la mitad de la
cantidad inicial. Esto es si llamamos a T al tiempo medio de
dicha sustancia, entonces T debe satisfacer la ecuación |
|
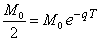
|
| despejando T, obtenemos |
|
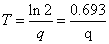
|
| Observemos que está última ecuación nos permite
expresar la constante de proporcionalidad q en función de la
vida media T, en efecto |
|
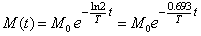
|
| A modo de ejemplo, se sabe que el radio 224 tiene un
tiempo de vida medio de 3.6 días, de modo que |
|
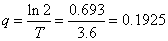
|
| y en consecuencia la evolución de la cantidad de masa
del radio 224 es |
|

|