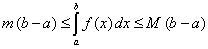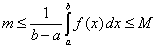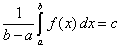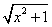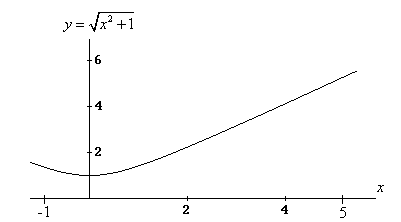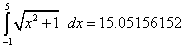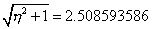| Consideremos una función f( x ) continua
en el intervalo [a, b]. Sean m y M el menor y el mayor
valor para la función f( x ), es decir |
|

|
| entonces podemos concluir que |
|
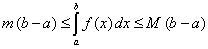
|
| de otra forma |
|
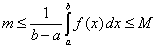
|
| Insistamos que el miembro derecho de esta desigualdad es
un valor real, por ejemplo |
|
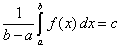
|
| de modo que este valor c se encuentra entre m
y M, y puesto que la función f( x ) también se
encuentra entre esos valores y además es continua, entonces
necesariamente habrá un valor, digamos h, en
el intervalo [a, b] tal que f( h
) = c, esto es |
|

|
| Es decir, el área determinada por la curva f( x)
y el segmento [a, b] es igual a un rectángulo de base (b
- a) y altura f( h ) para algún h
entre a y b. |
| Veamos el siguiente ejemplo. Sea la función |
|
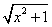
|
| definida entre -1 y 5, y cuya gráfica es |
|
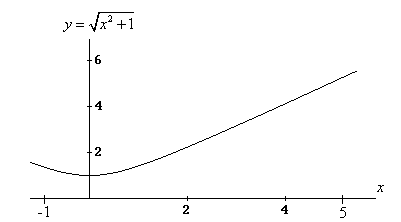
|
| La integral entre -1 y 5 es |
|
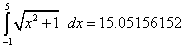
|
| de modo que debemos encontrar un valor de h
entre [-1, 5] tal que |
|

|
| De otra forma debemos resolver la ecuación |
|
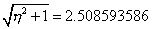
|
| Y esta solución es sencilla. En efecto, en este caso la
única solución en [-1 , 5] es h =
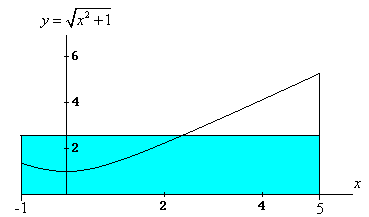
2.300661161. La situación gráfica es como sigue |
|
|
| donde el rectángulo de color celeste tiene base 6 y
altura 2.508593586, y su área es igual al área bajo la curva entre -1
y 6. |