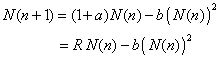| "Se sabe que, en algunas ocasiones, las especies
biológicas se comportan así, con alternancia de años de abundancia y
otros de escasez, fenómeno que estudió el matemático V. Volterra ya
en 1920, cuando un amigo pescador le explicó su sorpresa por las
oscilaciones en las capturas de algunas especies en el Adriático" Antonio
F. Rañada. Movimiento Caótico, del libro Orden y Caos. Edit. Prensa
Científica. Barcelona, 1990. |
| Vamos a estudiar la ecuación logística para el caso
discreto. Sabemos que el modelo logístico emerge de la ecuación
dinámica |
|
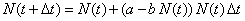 (1)
(1)
|
| Si trabajamos en tiempo continuo es cuando tenemos que
hacer Dt muy pequeño, pero si
trabajamos en tiempo discreto, esto es la unida de tiempo es mes, año
semana, etcétera sin permitir fracciones de esa unidad, es que hacemos Dt
= 1, y además por notación clásica t = n. De modo
que la ecuación en (1) queda como |
|
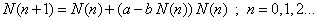
|
| La ecuación anterior la podemos arreglar como |
|
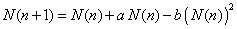
|
| esto es |
|
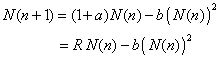
|
| si hacemos R = 1 + a. Ahora factorizando
nos queda |
|
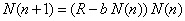 (2)
(2)
|
| Definamos el siguiente escalamiento de N ( n
) para todo tiempo n: |
|
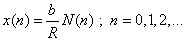 (3)
(3)
|
| de modo que si multiplicamos por b / R
la ecuación en (2) nos queda |
|
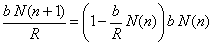
|
| y reemplazando por el escalamiento en (3) obtenemos
finalmente |
|
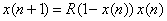 (4)
(4)
|
| Y la ecuación en (4) es la llamada ecuación logística
discreta. |
| ¿Qué significa la expresión x( n ) ?. De
la ecuación (3) observemos que el factor R / b = (1+ a) / b
y este factor es claramente mayor que la "carga" k = a
/ b, esto es la capacidad máxima que puede soportar el nicho
ecológico, de modo que x( n ) viene a ser una suerte de
densidad poblacional que oscila entre 0 y 1. |
| Por otro lado, para que la densidad poblacional de la
próxima generación, esto es x ( n + 1 ) también se
encuentre entre 0 y 1 el factor R debe satisfacer que 0 < R
< 4. En efecto, la parábola (1 - x ) x alcanza su
mayor valor en 1 / 4, y puesto que necesariamente 0 < R x
( 1 - x ) < 1 entonces debe ocurrir que 0 < R <
4. |
| Lo que debemos hacer es entregar valores para el
coeficiente R (entre 0 y 4) y veremos porqué ciertas especies
oscilan de temporada en temporada de abundancia a escasez. |