La integral como área bajo la curva
|
| 1. Encontrar las áreas cerradas formadas por el eje x y
la curva y = (x + 3)(x - 2)(x - 5) |
| 2. Encontrar el área acotada por la curva y = (1
- x)2 y la recta y = 4 |
| 3. De las áreas asociadas con las siguientes integrales,
probar que |
|
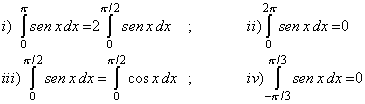
|
| 4. Encontrar el área acotada por y = x(x
- 1)2 ; y = 0; x = - 1/2; x = 1 |
| 5. Encontrar en área acotada por y = 2 + x2,
y = 0, x = 1, x = 4. |
Aplicación del valor medio para integrales
|
| 6. Encontrar los valores de h
y f( e ) = h en el
teorema del valor medio para integrales en cada uno de los siguientes
casos: |
| i) f( x ) = e2x en el
intervalo [0,
1]
ii) f( x ) = x3 en el intervalo [0, 2] |
| iii) f( x ) = x1/2 en el
intervalo [1,
2]
iv) f( x ) = sen ( p x
/2 ) en el intervalo [0, 1] |
Integrales y derivadas
|
| 7. Demostrar por derivación que |
|
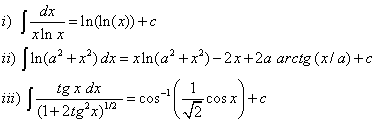
|
| 8. Encuentre el valor de la función que satisface la
siguiente ecuación diferencial |
|
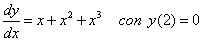
|
| 9. La aceleración de un coche como función del tiempo
está dada por |
|
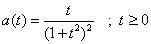
|
| Encontrar la velocidad y la distancia recorrida como
función del tiempo si ambas son ceros en t = 0. |
| 10 la velocidad de un automóvil está dada por |
|
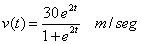
|
| Encuentre la distancia recorrida entre t = 1.5 y t
= 6.2 |