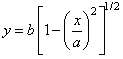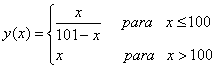| 1. Encontrar el mayor rectángulo que puede ser inscrito
en el área acotada por el eje y = 0 y la semi-elipse |
|
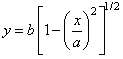
|
| 2. Una firma desea poner el precio a un libro
tecnológico de tal modo de maximizar las utilidades. El costo de
producción y el marketing, en dólares, obedece a la función |
|
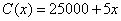
|
| donde x es el número de libros vendidos. Se pretende que
el precio del libro P se relacione con los libros vendidos mediante la
ecuación empírica |
|
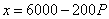
|
| de tal forma que el precio del libro no puede ser menor a
5 dólares (¿verdad?). ¿Cuál es el precio óptimo para asignar al
libro si queremos maximizar la utilidad? |
| 3. En un particular proceso de manufactura, se sabe que
el número de artículos rechazados y depende del total de
artículos producidos diariamente x, esto es y = y
( x ). La firma obtiene una utilidad de A por cada
artículo vendido bueno, pero pierde A / 3 por cada artículo
rechazado. ¿Cuál debería ser la producción diaria para maximizar las
utilidades? |
| 4. Para el problema anterior suponga que |
|
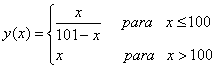
|
| ¿cuál debe ser la producción diaria? |