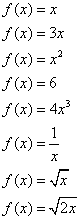| 1. Utilizando la definición de derivada, calcule en el
punto x la derivada de las siguientes funciones: |
|
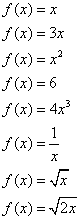
|
| 2. Grafique cada una de las funciones anteriores, y además
para cada función grafique la recta que es tangente a la gráfica de la
función en el punto (1, f ( 1 ) ). |
| 3. Calcule la función derivada de la función h ( x
) = x ( 1 - x ). Y evalúe la derivada de esta función en
el punto x0 donde la parábola obtiene su máximo valor. |
| 4. No tiene usted calculadora, y necesita calcular el valor
de (1,01)1/2. ¿Cómo encontraría un valor aproximado?
Indicación: Utilice la derivada. |
| 5. Un problema del Liceo: Un partícula lleva una velocidad
que se rige por la función v ( t ) = 3t + 2 metros /
segundo. Es decir desde un punto referencial que llamaremos origen en el
tiempo t = 0 se encontraba a dos metros de ese origen y en un
segundo estará a 5 metros en relación al origen, luego a los dos
segundos se encontrará a 8 metros del origen y así sucesivamente.
Calcule el cociente de Newton para la velocidad de esta partícula, ¿qué
interpretación le da usted a este cociente de Newton? |