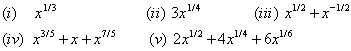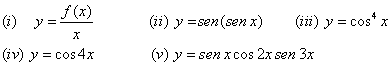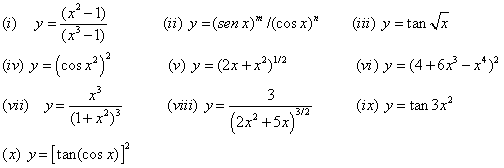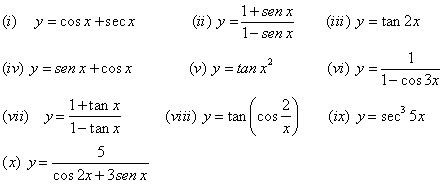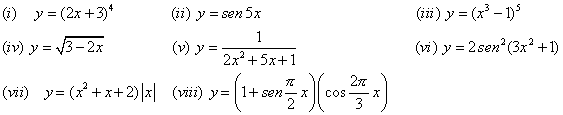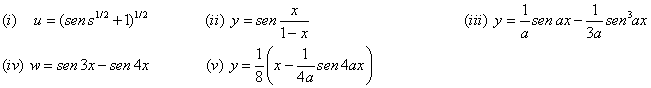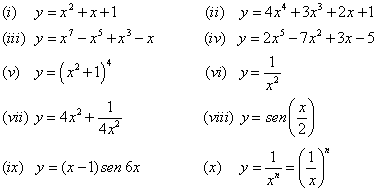Guía Nº 2

1. Derivar las siguientes funciones

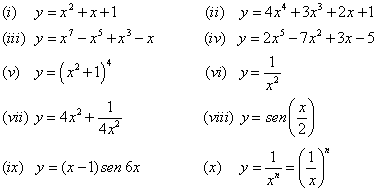
2. Derivar x1/3 mediante ( x1/3 )3 = x,  y luego usar la regla de la cadena.

3. Derivar x1/m, donde m es un entero, mediante la relación ( x1/m ) m = x.

4. Derivar xn/m usando la identidad xn/m = ( x1/m )n y el resultado del ejercicio 3.

5. Derivar las siguientes funciones

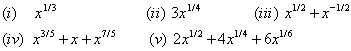6. Evaluar dy/dx para y = u2 + v2, donde u = cos f(x) y v = sen f(x), usando la regla de la cadena

7. Derivar (x3)1/2 mediante x3/2 = x x1/2 y aplique la derivada de un producto. Luego use la regla de la cadena para derivar (x3)1/2, y establecer el mismo resultado

8. Si f ( g(x) ) = x, encontrar g `( x ).

9. Derivar cada una de las siguientes funciones

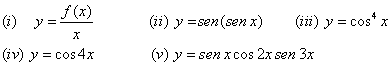10. ¿Para qué valores de x la pendiente de y = 1 / (sen x ) es igual a 1?

11. Derivar las siguientes funciones

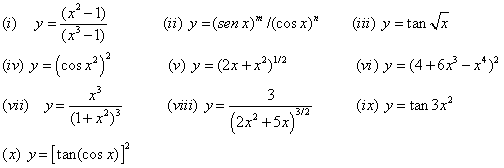12. Derivar cada una de las siguientes funciones

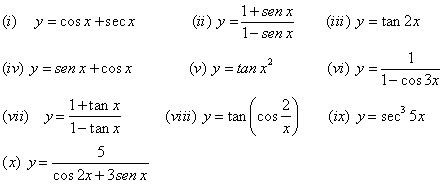13. Evaluar dy/dx para cada una de las siguientes funciones

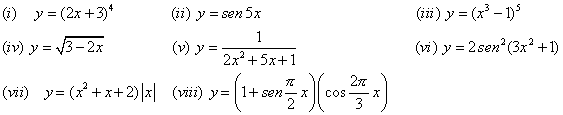14. Derivar cada una de las siguientes funciones

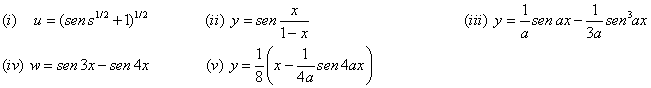15. La fuerza gravitacional por unidad de masa ejercida sobre un cuerpo por la tierra se describe por la ley del cuadrado inverso f = m / r2. Donde m es la constante gravitacional, y r la distancia del cuerpo al centro de la tierra. Considere que el radio de la tierra es de 3960 millas. Estime el cambio relativo en el peso de una persona que va sentada en un aeroplano que vuela a una altitud de 7 millas sobre el nivel del mar.

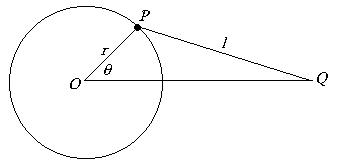
16. Los puntos P y Q de la figura siguiente están conectados por una barra rígida de longitud l; el punto P se mueve alrededor del círculo de radio r, pero Q está restringido a moverse a lo largo de la línea horizontal que pasa por O.

Si el ángulo q es variado levemente en una cantidad Dq, encontrar el correspondiente cambio en la distancia OQ.

17. El volumen de un cono circular recto de radio r está dado por V = (1/3)pr2h. Si la medición de r tiene un error del 4 por ciento y para h el error es del 1% , ¿cuál es el máximo error relativo para el volumen?

18. Computar aproximadamente mediante derivación lo siguiente:

(i) sen 32o          (ii) tan 43o               (iii) cos 59o

19. El volumen de una esfera es V = 4/3 p r3. Demostrar que dV = 4 p r3 e interpretar este hecho geométricamente mediante dos esferas concéntricas de radio r y r + dr.