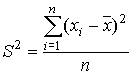
La cantidad S2 se llama varianza muestral y tiene un valor fundamental en el análisis estadístico, su interpretación es como sigue: es el promedio de las desviaciones cuadráticas respecto de la media.
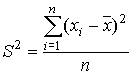
Si las observaciones están distribuidas en las clases c1, c2, ... ck entonces
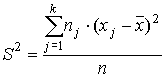
Se puede demostrar fácilmente que
.
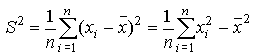Propiedades de la varianza.
Supongamos que tenemos las siguientes observaciones
x1, ..., xi, ..., xn,
cuya varianza la denotaremos por
.
Supongamos que sobre cada una de estas observaciones realizamos la siguiente
transformación
Entonces para estas nuevas observaciones transformadas linealmente calcularemos su varianza, esto es
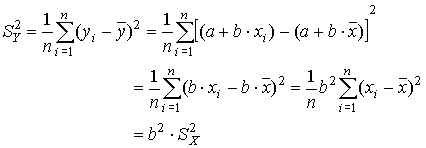
Resultado muy lógico a pesar de lo extraordinario. Notemos
lo siguiente, que si tenemos una serie de observaciones, a saber
,
entonces si hacemos un "traslado" de todas estas observaciones a una
distancia que nos interesa, como por ejemplo
entonces lo que nos dice la propiedad anterior, que la varianza es la misma que las observaciones anteriores. Es decir que si trasladamos "conjuntamente" las observaciones a otro sitio, las observaciones siguen manteniendo el mismo grado de dispersión.
Finalmente, si hacemos un cambio de escala, es decir multiplicamos cada una de las observaciones por una cantidad constante, entonces la varianza de este cambio de escala será proporcional a la anterior en un factor cuadrático de la cantidad constante.
La siguiente propiedad es de suma importancia. Supongamos que tenemos los siguientes datos estadísticos distribuidos de la siguiente manera:
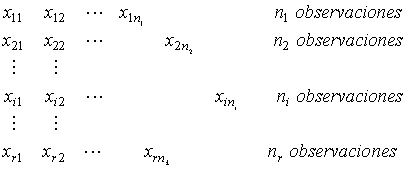
Supongamos que cada fila tiene media 
y
varianza
, con 
.
Entonces la varianza de todas observaciones que son 
satisfacen la siguiente relación
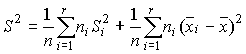
Veamos su
demostración. La varianza total de las 
observaciones,
con
; 
es
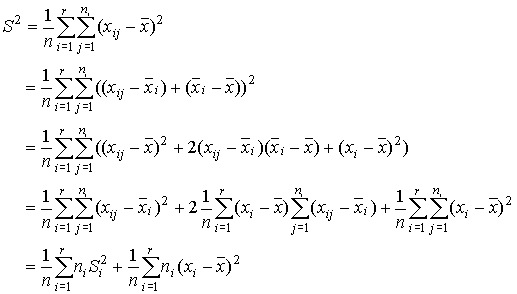
Una última propiedad de la varianza que daremos sin
demostración es la siguiente: Si tenemos las observaciones,
entonces en el intervalo real 
se
encuentra al menos el 75% de las observaciones.