Los percentiles, como veremos en un momento, entregan la idea de "posición" de los datos, es decir avisan a partir de que observación o intervalo de clase se ha acumulado un determinado porcentaje de observaciones. Es decir, cuando hablemos de percentil de orden k, significa que debemos identificar una observación (caso discreto) o un intervalo de clase (caso continuo) de tal manera que la frecuencia asociada a ese valor lleva acumulado el k% de las observaciones.
El percentil de orden k, se denota por Pk, y en el caso discreto es la observación cuya frecuencia absoluta acumulada alcanza el valor igual el k% de las observaciones. En el caso continuo, se trata de encontrar el intervalo ( li -1, li ], tal que su frecuencia absoluta acumulada Ni sea la primera frecuencia que satisfaga
![]()
donde n es el número de observaciones. De manera análoga a como calculamos la mediana, puesto que la mediana es un particular percentil, en rigor es el percentil de orden 50, se calcula la observación dentro del intervalo en que se encuentra el percentil. Este cálculo nos entrega el siguiente percentil de orden k:
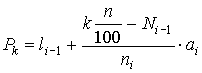
que se obtiene observando el siguiente gráfico
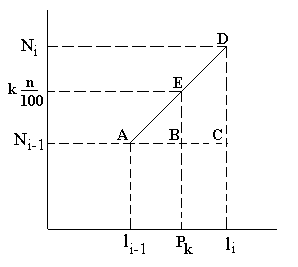
Los percentiles de mayor importancia son los cuartiles, que son tres percentiles que van "segmentando" las observaciones de 25% en 25%, y se denotan por Q1, Q2 y Q3, y se definen como
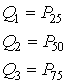
Lo otros percentiles importantes son los deciles, que van dividiendo a las observaciones de 10% en 10%, se denotan por Di, con i = 1, ..., 9; y se definen por
![]()
Ejemplo
1. Se entrega a continuación una tabla de observaciones correspondiente a un caso discreto, en que se consulta sobre el número de hijos a 100 familias
|
Número de hijos |
Frecuencia absoluta |
Frecuencia acumulada |
|
0 |
14 |
14 |
|
1 |
10 |
24 |
|
2 |
15 |
39 |
|
3 |
26 |
65 |
|
4 |
20 |
85 |
|
5 |
15 |
100 |
|
n = 100 |
Se pide calcular los cuartiles.
El primer cuartil, Q1, se obtiene observando en la columna de frecuencia acumulada el primer valor que sea igual o supere a la cuarta parte de las observaciones, esto es n/4 = 100/4 = 25; y esta frecuencia es N3 = 39, según la tabla, y a este valor está asociada la observación x3 = 2. De manera que Q1 = 2.
El segundo cuartil se obtiene de manera similar. La primera frecuencia absoluta acumulada que supera el 50% de las observaciones es N5 = 65 > 50, y a esta frecuencia absoluta está asociada la observación x4 =3, de modo que Q2 = 3.
De igual manera se puede calcular que el tercer percentil es Q3 = 4..
2. Calcular los cuartiles para la siguiente tabla de distribución correspondiente a observaciones continuas,
|
Intervalos de clase |
ni |
Ni |
|
[0, 1] |
10 |
10 |
|
(1, 2] |
12 |
22 |
|
(2, 3] |
12 |
34 |
|
(3, 4] |
10 |
44 |
|
(4, 5] |
7 |
51 |
|
Total |
n = 51 |
Vamos al cálculo del primer cuartil. Puesto que hay 51 observaciones, debemos encontrar el primer intervalo en que su frecuencia acumulada es igual o supera al 25% de las observaciones, es decir a 51/4 = 12,75. Este intervalo es c2 = (1, 2], cuya frecuencia acumulada es N2 = 22. De manera que el primer cuartil se obtiene mediante la fórmula
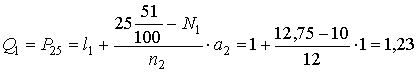
El segundo cuartil se obtiene encontrando la primera frecuencia acumulada que supera a 51/2 = 25,5. Esta es N3 = 34, correspondiente al intervalo (l2, l3] = (2, 3]. Aplicando la fórmula adecuadamente, nos queda
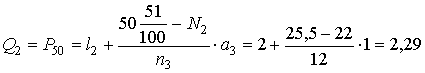
El tercer cuartil se calcula de manera análoga, y su resultado es Q3 = 3.445..