

El biólogo, y además uno de los fundadores de la Teoría General de Sistemas, Ludwing Von Bertalanffy desarrollo un modelo de crecimiento en función del tiempo de vida, que es un modelo de tipo exponencial para el crecimiento individual y que es aplicado a la gran mayoría de peces. He aquí el modelo matemático:
L(t) = Lmax (1 - e(- k ( t - t0) ) (1)
Los valores involucrados en esta ecuación son: L(t), talla en el tiempo t de la especie; t, edad de la especie; Lmax, es la talla máxima permisible en la especie, o de otra forma es la talla media de un pez "muy viejo"; k es un "parámetro de curvatura", y que como veremos más adelante tiene unidades de frecuencia (1/tiempo). Finalmente, t0 es el "parámetro de condición inicial" y no tiene un significado biológico directo, puesto que necesariamente debe ser negativo, si bien es cierto que su unidad es la unidad de tiempo (por lo general años), ya que si no es negativo, entonces la variable t que indica la edad del pez en algún momento alcanzará el valor de t0 (si lo suponemos positivo), y en ese valor tendríamos el absurdo que L(t0) = 0
Para familiarizarnos con la curva dada en (1) supongamos los siguientes valores para los parámetros
Lmax = 50 (cms); k = 0.5 (1/año); t0 = - 0.2 (años)
De modo que, para un mismo pez, los siguientes datos representan la evolución de su crecimiento a través de los años:
|
edad del pez (años) |
talla del pez |
| 0.5 | 14.7655 |
| 1 | 22.5594 |
| 1.5 | 28.6292 |
| 2 | 33.3564 |
| 2.5 | 37.0379 |
| 3 | 39.9051 |
| 3.5 | 42.1381 |
| 4 | 43.8771 |
| 4.5 | 45.2315 |
| 5 | 46.2863 |
El modelo presentado en (1), es bastante utilizado en las investigación de recursos pesqueros, incluyendo en este modelo a especies de moluscos.
El papel de la constante k
El siguiente gráfico muestra el comportamiento del modelo (L, la talla en centímetros, y t en años)
L(t) = 50 (1 - e(- k ( t + 0.2) )
para tres diferentes valores de k.
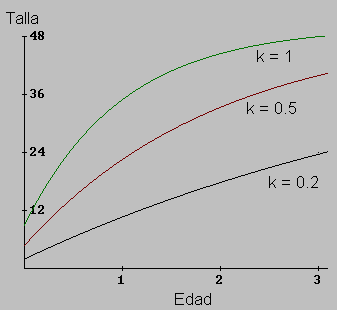
Analíticamente, y confirmado a través del gráfico, la constante k es crucial en la tasa de crecimiento del pez. Veamos cómo encontramos su estimación a la luz del modelo (1).
La función L(t), aceptando que representa biológicamente el crecimiento (la talla) de una especie a través del tiempo, y aceptando de manera natural que este crecimiento no es constante puesto que la propia talla de la especie regulará su crecimiento, podemos concluir la siguiente ecuación dinámica:
L(t + Dt) = L(t) + (a + bL(t))Dt (2)
Digamos que la constante a es una tasa "normal" de crecimiento, donde a > 0, y esta constante de crecimiento es "retardada" por la propia talla, y que supondremos que el "efecto de retardo" será proporcional a la talla anterior, de modo que la expresión completa "a + bL(t)" es la tasa de aumento de la talla, donde b < 0 (para que tenga el efecto de reducir el valor de a), y las unidades de a y b son cms/año (rapidez) y 1/año (frecuencia), respectivamente.
De la expresión (2) podemos concluir que el aumento por unidad de tiempo es
![]() (3)
(3)
y el primer miembro de esta última igualdad, para Dt pequeño, es igual a la derivada dL(t)/dt, y esta se obtiene derivando la función dada en (1), que es
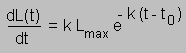
y además de (1) también se desprende la igualdad
![]()
de modo que se concluye que
![]() (4)
(4)
y puesto que teníamos que DL / Dt = dL(t) / dt (aproximadamente cuando Dt es pequeño), de (3) y (4) tenemos que
![]() (5)
(5)
Comparando (5) y (3) podemos concluir que,
Lmax = - a / b
K = - b
Nota: puesto que b < 0, es fundamental el signo menos. Por otro lado la ecuación (3) es una recta, y si consideramos una nube de valores para (DL / Dt, L(t)), podemos estimar a y b mediante la técnica de mínimos cuadrados, y de esta manera obtener estimadores para k y Lmax.
Estimación de K y Lmax
Como lo expresamos anteriormente, aprovecharemos la estructura lineal de la expresión (3) para estimar mediante mínimos cuadrados los valiores de a y b, y luego entonces obtener k y Lmax.
Supongamos que se ha estudiado la evolución de un pez, durante siete años midiendo cada año su talla. Los datos son
| edad | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| talla | 25.7 | 36.0 | 42.9 | 47.5 | 50.7 | 52.8 | 54.2 |
Para obtener la nube de datos (DL / Dt, L(t)) realizaremos la siguiente metodología. Para cada par de tiempos correlativos, calcularemos DL / Dt; y a su vez, para el intervalo de tiempo [t, t + Dt] calcularemos la talla correspondiente a es intervalo mediante una interpolación simple, esta es la del punto medio, de otra forma
![]()
será el valor asociado a la razón de crecimiento
![]()
| 30.9 | 39.5 | 45.2 | 49.1 | 51.8 | 53.5 | |
|
|
10.3 | 6.9 | 4.6 | 3.2 | 2.1 | 1.4 |
Se deja al estudiante los cálculos de la estimación de a y b en mínimos cuadrados, y por ende las estimaciones de k y Lmax.
continuará...