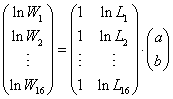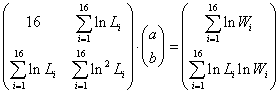Modelos lineales: modelos "linealizables"

La densidad de un elemento, o de un sistema de elementos que llamaremos cuerpo, se define como el cociente entre la masa y el volumen que tiene y ocupa el cuerpo (sea  en el estado que se encuentra el cuerpo o sistema), esto es:

Si este cuerpo es compacto, es decir que tiene una masa homogénea, podemos pensar en un cubo de hielo a manera de ejemplo, tendremos que su densidad es constante. Ahora bien, por lo general, es más sencillo determinar el peso antes que la masa del cuerpo (recuerde que el peso es igual a la masa por la aceleración de gravedad), entonces el cociente entre peso y volumen se conoce como peso específico, esto es

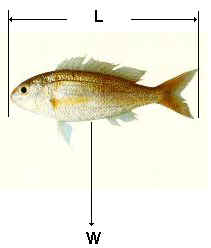
Si suponemos que este peso específico, que llamaremos p es constante, tenemos que el peso, W, y el volumen V, se rige por la relación

W = p V

Ahora bien, consideremos que el cuerpo que estamos estudiando es el indicado en la figura 1, el Nemipterus marginatus. Allí se entrega la longitud L, conocida como talla del pez N. marginatus.

Si consideramos el cubo de un volumen generado por la longitud L, este volumen será obviamente L³, luego el volumen real del pez será una fracción, digamos r de este volumen. De manera que estamos tentados a decir que la relación entre el peso y la talla del N. marginatus está dada por

W = k L^{3      (1)}

siendo k una constante determinada por el producto entre el peso específico y la fracción r.

Ahora bien, en la literatura clásica sobre la evaluación de recursos pesqueros se asegura que la relación talla y peso (específicamente para el N. merginatus) obedece a un modelo de la forma

W = q L^{b         (2)}

El problema es ¿cómo elegimos los parámetros q y b del modelo propuesto?. La respuesta es sencilla. Aplicando logaritmo a (2) nos queda

ln W = ln q + b ln L

Si hacemos Y = ln W,  X = ln L,  con a = ln q, nos queda la ecuación de una recta,

Y = a + b X

Figura 1.

Ahora, para estimar los parámetros a y b planteamos las ecuaciones normales y resolvemos. La matriz de diseño se obtiene de

De manera que las ecuaciones normales quedan como

En nuestro caso, con los valores de L_i y W_i las ecuaciones normales quedan como:

cuya solución es a = -4.537859957 y b = 3.057349930. De modo que el valor de q se obtiene resolviendo a = ln q, que es

q = 0.010696

De tal modo que el modelo propuesto es

W = 0.00107 L^3.057         (3)

a continuación presentamos los valores de W_i (de los pesos de los N. marginatus)  y los W_teo entregados por el modelo dado en (3),

El eee para este modelo es 6.489687899, que es menor que los errores de estimación estándar de los otros dos modelos anteriores, de manera que nos quedamos con el modelo (3).