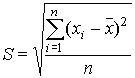Desviación estándar

En rigor, esta medida de dispersión es utilizada con más frecuencia por los estadísticos. Supongamos las observaciones x₁, .., x_i, .., x_n, entonces la desviación estándar S se define como

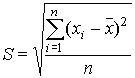(1)

Observemos como antes que esta desviación estándar tiene la misma unidad que las observaciones. En rigor es un promedio de las diferencias cuadráticas de las observaciones respecto de la media. El cuadrado permite eliminar los signos negativos, de modo que no se anulen diferencias simétricas en torno de la media. Ahora, en realidad esta expresión tiene profundas raíces en el Análisis Geométrico. En efecto, si tenemos un punto en el espacio plano, por ejemplo (y₁, y₂) entonces podemos medir la distancia que hay desde este punto al origen  utilizando la relación pitagórica

cuya interpretación geométrica es evidente según la siguiente gráfica

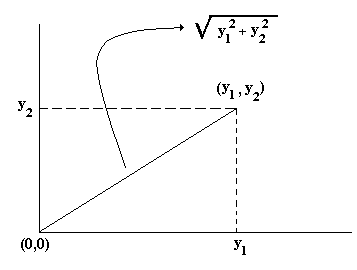
Esta idea de distancia la podemos extender a un punto en el espacio n-dimensional, entonces el "punto" (y₁,..., y_i, ..., y_n) respecto del "origen" (0,..., 0, ..., 0) tiene una distancia igual a

y conforme esta expresión tenga un valor pequeño o grande se dice que el punto está cerca o lejos del origen, respectivamente. Ahora bien, podemos considerar las observaciones (x₁, ..., x_i, ..., x_n) como un punto en el espacio n-dimensional, y en particular formamos un nuevo punto en que a cada componente le restamos la media, esto es

De manera tal que necesitamos saber si este punto está alejado del origen o no, de otra forma necesitamos calcular su distancia respecto de origen, esto es

Comparando esta expresión, que tiene un claro significado geométrico, con la expresión dada en (1) podemos concluir que la desviación estándar es simplemente una distancia, y que el término de división por es simplemente una suerte de normalización (perfectamente no se podía haber dividido o dividir por ejemplo por)