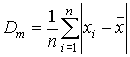
Hasta ahora hemos estudiado en las observaciones los estadísticos de posición (percentiles) y de tendencia central (medias, medianas y modas). Sin embargo debemos tener una noción en cuanto a la relación existente entre estas observaciones, una medida de cuan alejada está una determinada observación del resto, o de una medida de disgregación que tienen estas observaciones. En rigor la primera medida de dispersión que ya hemos estudiado es el rango de las observaciones. Pero es claro que esta medida presenta varios inconvenientes. En primer lugar solo considera dos observaciones, la más pequeña y la mayor, de modo que no puede ser muy fiable toda vez que uno de estos valores extremos se aleje demasiado y el resto se encuentre muy agrupado. En segundo lugar, podemos aumentar el número de observaciones, esto significa tener más precisión en el fenómeno en estudio, y es posible que las nuevas observaciones se agrupen, por ejemplo en torno a la media, y el rango no disminuirá. Finalmente, basta que una observación nueva sea mayor o menor que el resto de las anteriores para que el rango aumente. De manera que es conveniente que creemos otras medidas de dispersión.
Supongamos que tenemos las observaciones no necesariamente ordenadas x1, x2, ..., xi, ..., xn. Se define entonces la desviación media, Dm, como
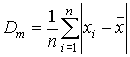
esto es, el promedio de las distancias de cada observación respecto de su media. Si los datos están agrupados en k intervalos de clases C1, C2, ..., Ck, y tenemos las correspondientes frecuencias absolutas, ni por clase, entonces
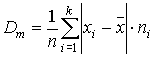
Se debe notar que la unidad de esta desviación media tiene la misma unidad que las observaciones.