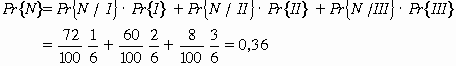Es sin duda este teorema el caballo de batalla de los procesos estocásticos, es decir de procesos que toman resultados aleatorios a través del tiempo, y es el soporte para el controvertido Teorema de Bayes. Basta de preámbulos y veamos de que se trata.

Supongamos que para el espacio tenemos definida una "partición" sobre, digamos, de tal modo que se conoce cada probabilidad para i variando de 1 a n. Consideremos un suceso A de este espacio de probabilidad, y además supongamos que se conoce para cada i. Entonces la probabilidad se determina mediante:

(1)

Recordemos que una partición sobre un conjunto significa una colección de subconjuntos cuya reunión forma el conjunto particionado, pero estos subconjuntos no tienen elementos en comunes. Piense en las provincias de un país, como paradigma de partición (de un país). De manera que se interpreta por lo que es, la probabilidad de A condicionado a la ocurrencia del suceso A_i. Otra manera de interpretar esta expresión es: es la probabilidad de A "bajo el escenario A_i". Y cada es la probabilidad de cada escenario, de manera que lo que dice la formula anterior (1) es lo siguiente: La probabilidad de A es igual a la suma de todas las probabilidades de A condicionados al escenario A_i por la probabilidad de que ocurra el escenario A_i.

Imagínese usted la siguiente situación. Hay tres urnas como se indica en el esquema siguiente. Para cada urna hay una determinada distribución de bolitas negras y blancas, y que también se indica en el esquema

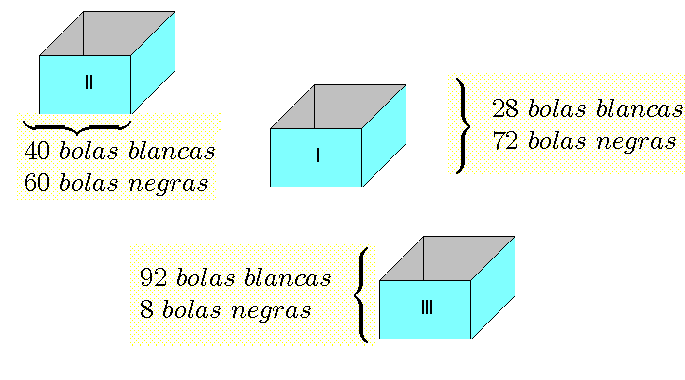
Supongamos que la probabilidad de cada urna se define como:

Entonces la probabilidad de que la bola sea negra está dada por