Eliseo Martínez H.
Introducción.
Los fundamentos de la dinámica de sistemas, creados por Jay Forrester, se están extendiendo cada vez más entre nuestros estudiantes, donde la expresión “extendiendo” la utilizamos en el amplio sentido de “conociendo y aplicando”. Hay sobrados ejemplos de fundamentos teóricos que son comprendidos en la etapa de aprendizaje, pero posteriormente no son aplicables. No queriendo con esto decir que ha sido un “aprendizaje inútil”, sino que simplemente no se utiliza en la mayoría de las veces a causa de su rango de validez. Por ejemplo nadie duda de la potencia de la Transformada de Laplace para la resolución de ecuaciones diferenciales “lineales”, y es así que toda vez que aparecen ecuaciones diferenciales no-lineales (las más abundantes en la complejidad de hoy) los fundamentos y teoremas de la Transformada de Laplace quedan en el olvido, y con el agregado de que eventualmente “esa” ecuación diferencial no-lineal también quede en el olvido.
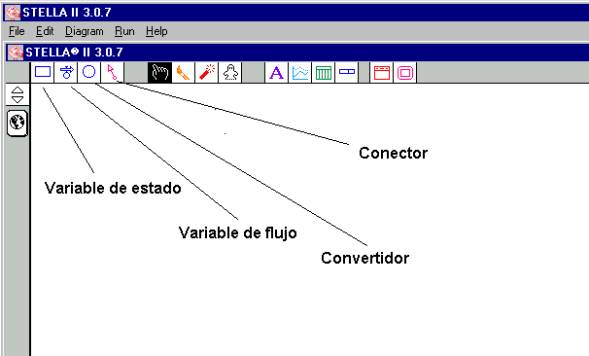
Pues bien, la dinámica de sistemas se basa en un lenguaje formal bastante simple, y en la que inicialmente podemos reconocer cuatro tipos de elementos: variable de estado, variable de flujo, convertidor y conector. Observe la figura 1 otorgada por el software STELLA (versión 3.07)
Si en un sistema dinámico, en su proceso de modelación, no se discrimina entre todas las variables del sistema que entrarán a formar parte del modelo, como variable de estado y como variable de flujos, de otra forma, si no se sabe cuales de las variables son de estado y cuales son de flujo, entonces simplemente no se podrá modelar el sistema dinámico. Así de simple.
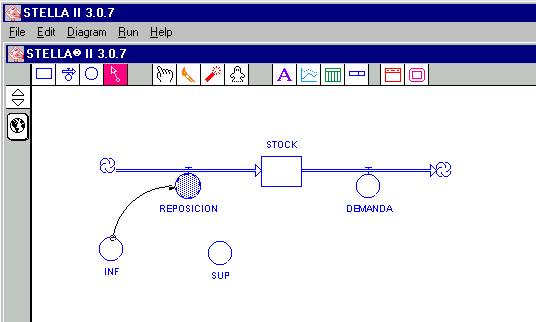
Conceptualmente una variable de estado es un stock que es alimentado por una variable de flujo o varias variables de flujo (de entradas), y que eventualmente puede ser vaciado por una o varias variables de flujo (de salidas); y así que las variables de flujo se definen como aquellas que alimentan o vacían el stock. Para fijar ideas supongamos que tenemos un sistema sencillo, por ejemplo una pequeña tienda de alquiler de automóviles en la cual al final de cada semana se reponen los automóviles, con una determinada política que veremos más adelante, para enfrentar la semana que viene caracterizada por una determinada demanda, que también veremos como se comporta más adelante. En definitiva, tenemos la variable de estado que llamaremos STOCK, y dos variables de flujo, un flujo de entrada que llamaremos REPOSICIÓN, y un flujo de salida que llamaremos DEMANDA. Notemos antes que nada que la unidad de la variable STOCK es “automóviles”, y las unidades de los flujos REPOSICIÓN y DEMANDA es “automóviles por semana”, de otra forma “automóviles/semana”. Vamos a dibujar la relación entre estas tres variables en STELLA,
Figura
2
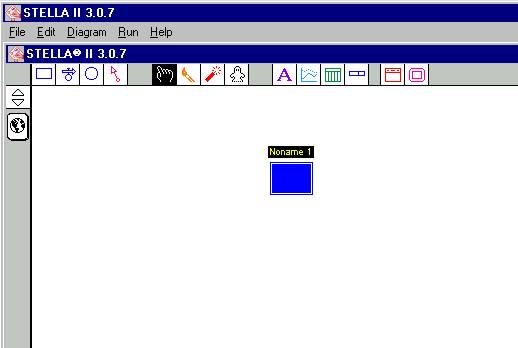
Con el cursor hacemos click con el botón izquierdo en el
icono de la variables de estado
,
arrastramos la figura a un sitio determinado y hacemos nuevamente click con el
botón izquierdo del mouse, para fijar el icono de la variable de estado. La
operación final deberá lucir como la indica la figura 2. Enseguida, ponemos el
nombre de STOCK al icono cuyo nombre por defecto es “Noname 1”. Lo obtenido
deberá ser similar a lo indicado en la figura 3.
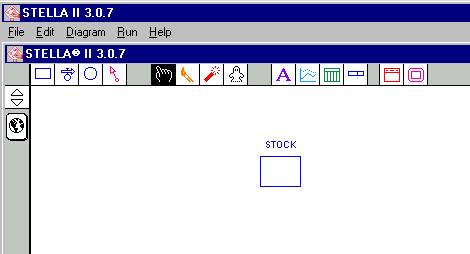
Figura
3
Ahora bien, vamos a dibujar el flujo de entrada hacía el STOCK. De manera análoga, dirigimos nuestro mouse hacia el icono de la variable de flujo, pinchamos haciendo un clic con el botón izquierdo, arrastramos la figura de manera conveniente, a la altura del lado izquierdo del STOCK, una vez elegido el sitio desde donde va a empezar a dibujarse la variable de flujo, presionamos el botón izquierdo (sin soltarlo) a la vez que arrastramos la figura dirigiéndola hacia el STOCK (figura 4), y toda vez que la variable de flujo llegue de manera adecuada al STOCK, este avisará con un leve cambio de color gris (figura 5), en ese momento dejamos de presionar el botón izquierdo y soltamos. La situación final debería lucir como lo indica la figura 6, toda vez que cambiemos el nombre por defecto de esta variable de flujo por el nombre definido anteriormente, REPOSICIÓN.
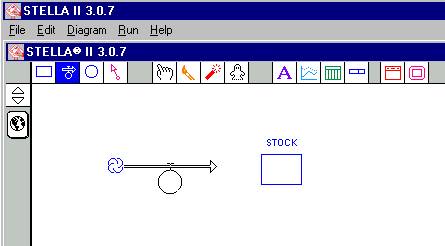
Figura
4
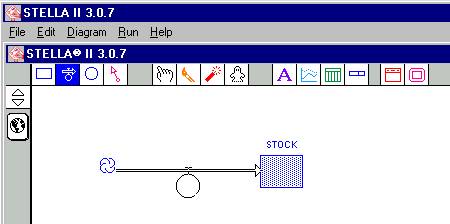
Figura
5
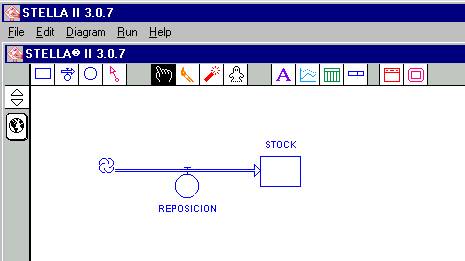
Figura
6
Para la
construcción de la variable de flujo que sale desde el STOCK, se realiza de
manera similar, esto es se hace un clic sobre el icono
, nos
ubicamos al interior de la variable de estado STOCK, presionamos el botón
izquierdo (sin soltar) y arrastramos el mouse hacia el lado derecho del STOCK,
cuando creamos conveniente detenernos, soltamos el botón derecho, y debería
aparecernos algo similar a la figura 7, toda vez que cambiemos el nombre que
viene por defecto por el de DEMANDA.
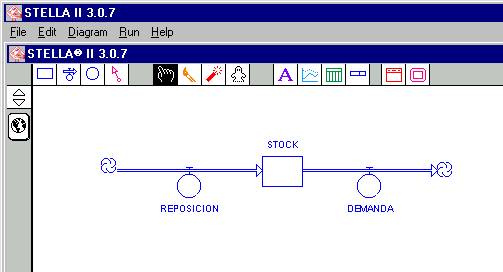
Figura
7
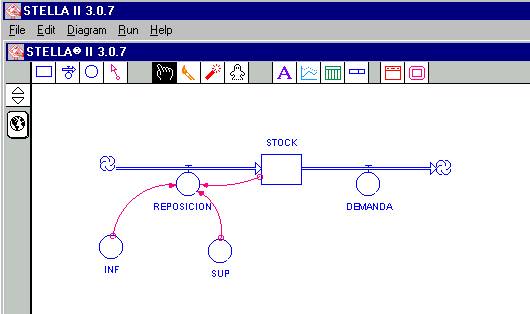
Este sencillo dibujo, nos muestra que la variación del STOCK a través del tiempo (semanas) será causada por los flujos de entrada (REPOSICIÓN) y salida (DEMANDA). Ahora bien, supongamos que esta demanda obedece una política de almacenaje conocida como “política (s, S)”, que consiste en lo siguiente: Al final de cada semana, si lo que hay en stock es inferior o igual que s unidades entonces inmediatamente se repone hasta el nivel S, en caso contrario, si lo que hay es superior al nivel s, entonces nada se repone. De manera que se introducen dos nuevas variables a nuestro modelos, a saber el nivel s, que llamaremos INF, y el nivel S, que llamaremos SUP. Estas variables no son ni de flujo ni de estado, para eso entonces utilizamos el icono de convertidores.
Con el mouse sobre el icono
hacemos
un clic, para coger la figura, y la posicionamos en un lugar adecuado nombrando
esta figura con el nombre de INF; repetimos el mismo procedimiento para definir
el convertidor SUP. El resultado final debería lucir como lo indica la figura
8.
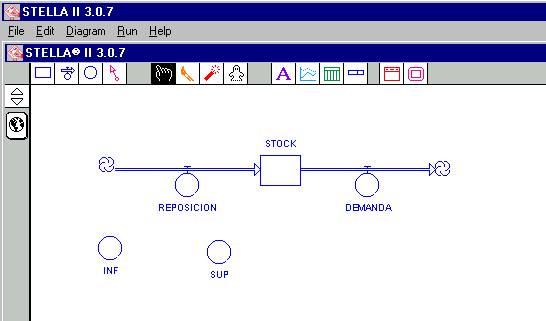
Figura
8
Ahora bien, vamos a indicar que el flujo de entrada
REPOSICIÓN depende de los valores de INF, SUP y finalmente del valor de la
variable de estado STOCK (en efecto, recuérdese que “si lo que hay en stock
es inferior o igual que s unidades entonces inmediatamente se repone hasta el
nivel S, en caso contrario, si lo que hay es superior al nivel s, entonces nada
se repone”). La manera de indicar esto es mediante los conectores. Y se
procede de la siguiente manera: nos posicionamos con el mouse en el icono
, para
capturar la imagen, y luego la ubicamos, por ejemplo, dentro de la variable INF
oprimiendo el botón izquierdo, sin soltar, y arrastrando el conector hacia la
variable de flujo REPOSICIÓN, dejamos de oprimir el botón derecho toda vez que
alcancemos a esta variable de flujo que lo indicará al cambiar a color gris.
Observe la figura 9.
Figura
9
Por último, mediante sendas operaciones análogas, conectamos desde las variables SUP y STOCK hacia REPOSICIÓN, y el resultado debería lucir como lo indica la figura 10.
Figura
10
Volvemos a insistir que el esquema indicado en la figura 10 nos dice que, los valores que tomará la variable de flujo REPOSICIÓN dependerán de los valores de INF, SUP y STOCK.
Continuemos con nuestro de almacenaje. Vamos a suponer que la demanda semanal es aleatoria con distribución conocida, y que además estas demandas semanales son independientes (en el sentido probabilístico) entre si. Supongamos que la demanda para cada semana se distribuye según una distribución de Poisson. Finalmente agreguemos que se entrega lo que hay en stock y no se acepta demanda diferida, esto es a modo de ejemplo, si hay en stock 2 unidades y la demanda en esa semana es de 5, entonces se entregan simplemente las 2 y no hay compromiso de entregar el resto de 3 unidades para la semana posterior. Con estos datos vamos a definir un convertidor llamado PEDIDO y otro convertidor llamado LAMDA. El convertidor PEDIDO, de alguna manera que ya determinaremos más adelante, va a simular los valores que se obtienen de una distribución de Poisson, y puesto que toda distribución dependerá de un parámetro (que indica el valor promedio de los números generados por esta distribución), llamaremos LAMBA a este parámetro. Finalmente debemos hacer notar que los valores generados por el convertidor PEDIDO dependerá de lambda, y todo valor que genere el convertidor PEDIDO se interpretará como la demanda ocurrida en esa semana. Entonces utilizando la técnica ya establecida dibujamos estas dos nuevas variables y establecemos los conectores para indicar las dependencia entre ellas. Observemos la figura 11.
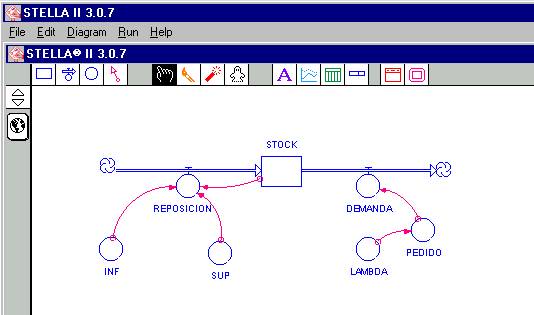
Figura
11
De manera que la figura 11 está indicando todos los elementos que integrarán nuestro modelo que representará el sistema de almacenaje o stock que opera con la política (s, S), y que tiene una demanda aleatoria distribuida independientemente según una Poisson. Y donde se indica las relaciones de independencia entre estos elementos (aún cuando, de momento, no se establece la relación analítica entre ellos).
Eliseo Martínez
Relaciones analíticas
Una vez que hemos “dibujado”
nuestro sistema-modelo de almacenaje, vamos a entregar las relaciones analíticas
establecidas entre las variables que están unidas por el conector. Observemos
atentamente el sector izquierdo de nuestro dibujo anterior, donde aparece el
icono
Figura 1
Si ubicamos el mouse sobre ese icono, y hacemos click con el botón izquierdo, tendremos la siguiente situación indicada en la figura 2.
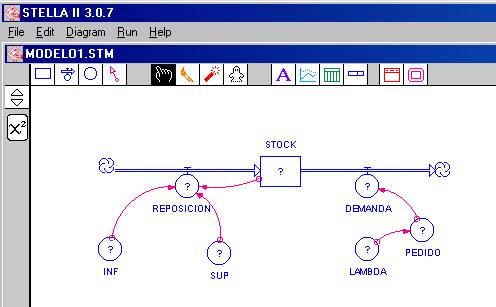
Figura 2
Los signos de interrogación que aparecen sobre las variables de nuestro modelo están indicando que sobre ellas hay que definir su relación analítica cuando corresponda, o entregar el valor que tienen. Vamos a fijar nuestra atención en la variable de flujo REPOSICION. Recordemos que ella está definida extensivamente como “toda vez que el valor del STOCK sea menor o igual que INF entonces se repone (de artículos) hasta el nivel superior SUP”. Bien, hagamos doble click sobre la variable de flujo REPOSICION, debe aparecer la siguiente caja de diálogo como se puede observar en la figura 3,
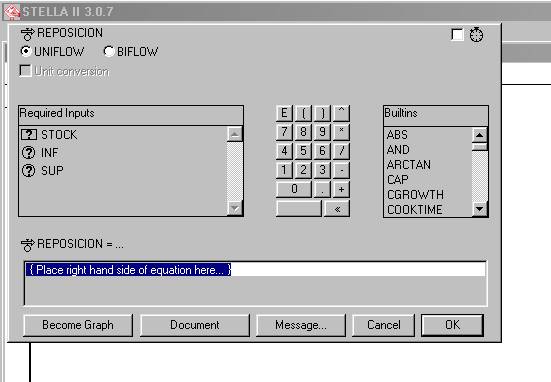
Figura 3
Sobre esta caja de diálogo haremos algunas precisiones. Hemos marcado cuatro sectores con rotulador de sendos colores, que llamaremos zona roja, azul, negra y verde, como lo indica la figura 4 que nos servirá para las precisiones respectivas.
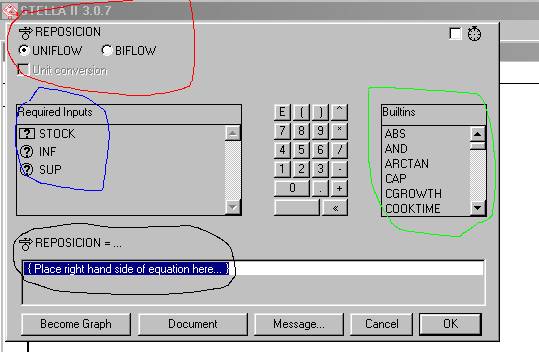
Figura 4
La zona roja nos indica que la variable de flujo, por defecto y conforme está activado el rótulo UNIFLOW, es un flujo unidireccional, esto es tiene la propiedad de que fluye “material” sobre la variable de estado (STOCK en nuestro caso) y que no tiene opción de “inhalar” material desde la variable de estado, en términos hidráulicos esta variable de flujo no puede bombear para extraer agua, solo puede depositar agua. Ya veremos más adelante algunos ejemplos en que una variable de flujo puede ser bidireccional. El caso es que nuestra variable de REPOSICION solamente entrega material hacia el STOCK.
La zona azul indica lo que ya hemos establecido, que sea la forma analítica que tenga nuestra variable de flujo REPOSICION, ella debe requerir para su definición las variables de STOCK, INF y SUP.
La zona negra está indicando la función analítica con la que quedará definida nuestra variable de flujo, y es en el lugar marcado por el video reverso donde dice “Place right hand side...” donde se debe poner la fórmula.
Finalmente la zona verde entrega una lista de funciones que posee en su estructura el software STELLA, en que eventualmente podamos necesitar para la construcción de la formula para la variable de flujo REPOSICION.
Vamos ahora a definir la variable de flujo. La expresión “toda vez que el valor del STOCK sea menor o igual que INF entonces se repone (de artículos) hasta el nivel superior SUP” es equivalente matemáticamente a lo que indica la figura 5:
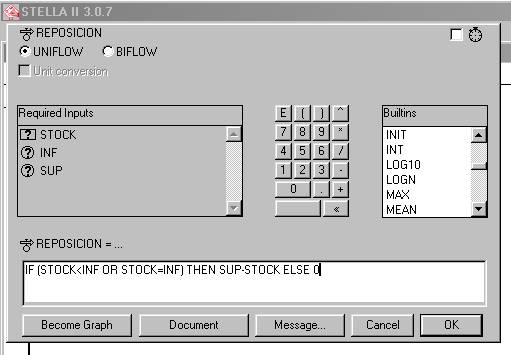
Figura 5
Una vez entregada esta instrucción, y convenciéndonos que es la adecuada para definir la política de reposición del stock hacemos click en la opción OK (los otros botones, como Become Graph, Document, etcétera, los veremos más adelante). Deberá aparecer el diagrama indicado en la figura 6, dónde ha desaparecido el signo de interrogación sobre la variable de flujo REPOSICION,
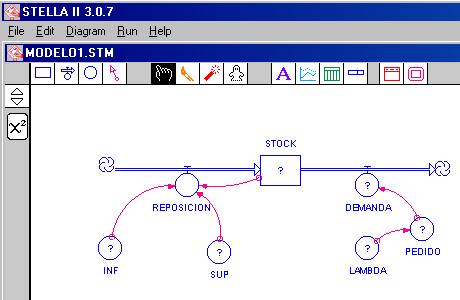
Figura 6
Ahora vamos a definir la variable de flujo (de salida) DEMANDA, haciendo doble click en esta variable, aparecerá una caja de diálogo similar al de la figura 3, y se indica en la figura 7.
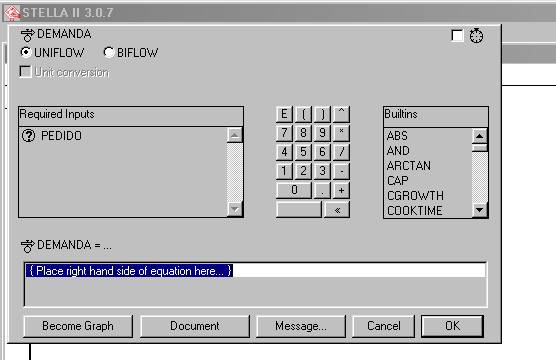
Figura 7
En este caso la variable de flujo DEMANDA solo dependerá de la variable PEDIDO, siendo esta una variable aleatoria con distribución conocida y que definiremos en su momento. De modo que simplemente hacemos un click en PEDIDO para hacer DEMANDA = PEDIDO, como lo indica la figura 8.
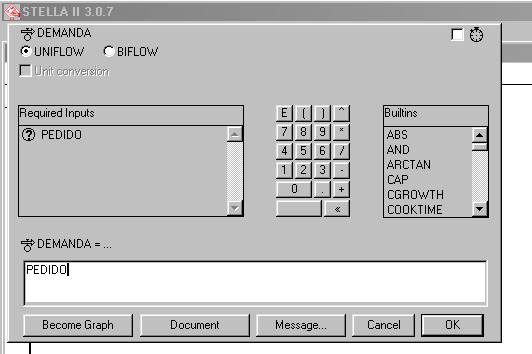
Figura 8
Nuevamente hacemos click sobre OK, para volver a nuestro diagrama donde se puede comprobar que habrá desaparecido el signo de interrogación sobre DEMANDA.
Ahora vamos a definir la variable aleatoria PEDIDO, que recordemos se distribuye según una Poisson de parámetro LAMBDA. Haciendo un doble click sobre PEDIDO, de la lista de funciones de la caja “Builtins” seleccionamos aquella que dice “Poisson”, y puesto que ella requiere del parámetro LAMBDA conforme se observa en la caja “Required Inputs” hacemos un click sobre LAMBDA, y nos queda lo indicado en la figura 9.
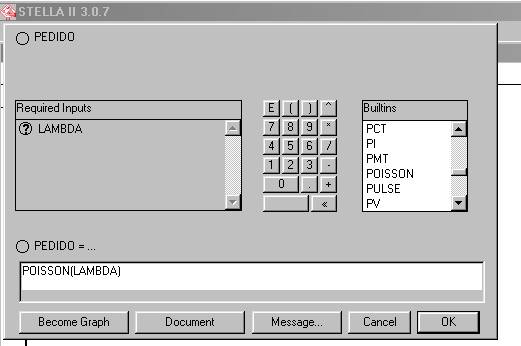
Figura 9
Supongamos ahora que en nuestro sistema de almacenaje o stock, el valor de INF tiene el valor de 1, SUP el valor de 3, y LAMBDA el valor de 1. Y además vamos a suponer que esta empresa de alquiler de automóviles empieza con el stock a nivel máximo, es decir con el valor de 3. La manera de entregar estos valores es simplemente hacer doble click en cada una de estas variables y entregar los correspondientes valores. Sin embargo dada su importancia vamos a efectuar el “llenado” de la variable STOCK. Observemos la figura 10.
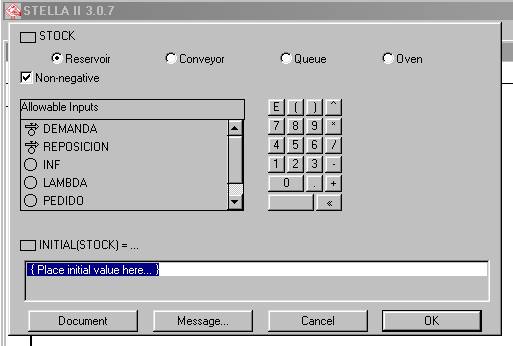
Figura 10
Observemos en la línea superior de esta caja de diálogo que por defecto está activado el botón “Reservoir” (Receptáculo), más adelante explicaremos las opciones “Conveyor, Queue y Oven”. Que sea esta variable de estado de la clases Reservoir significa literalmente que ella es un receptáculo que recibe flujo y que de ella puede emanar flujo, o de otra forma que su cambio de nivel (dinámica) o cambio de los valores de estados se debe solamente a los flujos, tanto de entrada o salida, que sobre ella operan, y que ninguna otra variable tendrá incidencia directa en su dinámica, esto significa que tampoco necesita conector alguno que provenga de otra variable que pueda modificar su comportamiento dinámico, es más, observe atentamente que no aparece la caja de diálogo “Required Inputs”, y en vez de ella aparece la caja “Allowable Inputs” y que en rigor son todas las variables que componen el modelo pero que no tienen ninguna relación analítica. Solamente hay que escribir el valor de INITIAL (STOCK), es decir solo debemos entregar su valor inicial, que en nuestro caso es 3. Escribimos este valor donde dice “Place initial value here” y hacemos click en OK.
Bien, ¿qué hemos hecho? La verdad es que hemos
realizado un programa computacional. En efecto, observe el icono
de la figura 1, y hagamos un click
en la flecha inferior, obtendremos el siguiente código computacional (figura
11)
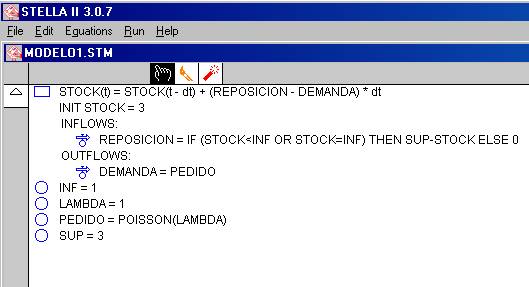
Figura 11
A este nivel, hemos realizado un programa computacional que nos permitirá hacer una simulación sobre el comportamiento del nivel de STOCK de una pequeña tienda de alquiler de automóviles. Observemos cuidadosamente estas ecuaciones para convencernos que efectivamente corresponden a un sistema de ecuaciones dinámicas que mostrarán la evolución a través del tiempo del sistema dinámico que estamos modelando.
Eliseo Martínez
Simulación
Vamos a enseñar como realizar simulación para el modelo que hemos realizado. Para esto, en el menú RUN elegimos la opción “Time Specs...”, como se ve en la figura 1,
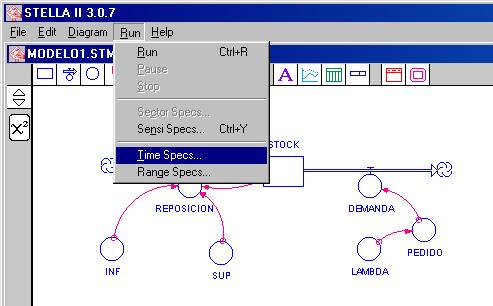
Figura 1
En esta opción vamos a determinar que el tiempo es discreto, toda vez que la evolución de este sistema es en tiempo discreto, en rigor la unidad de tiempo de “semana”, de modo que al hacer un click en la caja de diálogo que aparece lo completamos de la forma que lo indica la figura 2.
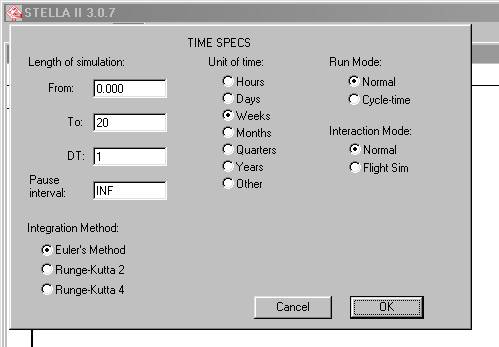
Figura 2
Como se puede observar, hemos determinado una longitud de
20 semanas, de manera arbitraria, con un DT igual a 1, y hemos elegido la unidad
de tiempo “Weeks” (Semanas). Una vez realizado esto hacemos un click en OK.
Con esto volvemos a nuestro diagrama original. Ahora bien, vamos a ver la
evolución de la variable STOCK mediante una gráfica, para esto hacemos un clic
en el icono
arrastrándolo a un sitio
conveniente, al fijarla aparecerá la siguiente caja de diálogo que indica la
figura 3,
Figura 3
Como podemos ver, solo en el eje vertical aparece la dimensión tiempo que hemos indicado anteriormente al definir la “longitud de la simulación”. Para poder definir la variable STOCK que queremos graficar hacemos doble click en cualquier parte gris de este plano cartesiano. Deberá aparecer la siguiente caja de diálogo
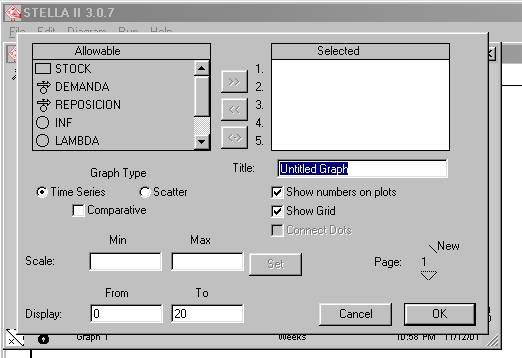
Figura 4
Como podemos observar, hay dos cajas principales, una que dice “Allowable” (Accesibles), y otra titulada “Selected” (Seleccionada). Como nuestro interés es graficar la evolución de la variable STOCK, es que seleccionamos esta variable haciendo doble click a STOCK en la caja “Allowable”, con esto logramos entonces que STOCK pase a la columna “Selected”. De momento solo elijamos esa opción y el resto de los botones, que están por defecto lo dejamos tal cual se ve en la figura 4. Una vez realizado esto hacemos un click en OK, y nos aparecerá la siguiente figura 5,
Figura 5
Y aquí podemos observar que el eje Y está tabulado con la variable STOCK. Nuevamente nos vamos al menú RUN y elegimos la opción RUN, debería aparecer una gráfica como la que indica la figura 6.
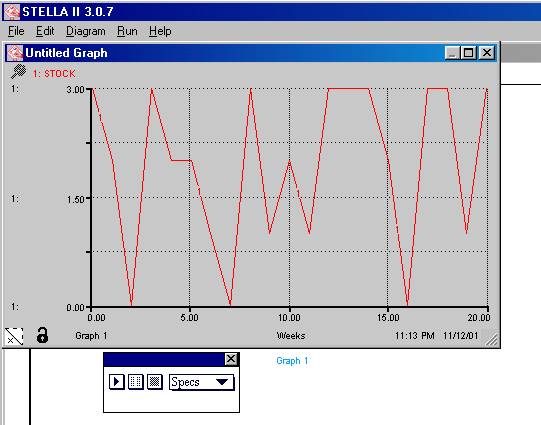
Figura 6
Esta gráfica nos entrega, entonces, una evolución dinámica
de la variable STOCK. Observe que ha aparecido una imagen similar a las que
tienen los controladores de “casette”. En efecto, ese es su papel. En los
iconos
, al presionar uno de ellos significan, “realizar una simulación”,
“pausa” y “detención”, respectivamente. La opción
al hacer click aparecerán tres
opciones como lo indica la figura 7.
Figura 7
La opción “Time Specs” nos llevará nuevamente a la caja de diálogo indicada en la figura 2 para una posterior cambio en los parámetros del tiempo (por ejemplo, aumentar la longitud de simulación). La opción “Sensi Specs” la veremos en una próxima sección. La opción “Range Specs” (Especificación del rango) sirve para indicar los límites del rango de, en nuestro caso, la variable STOCK.
Finalmente si queremos ver una tabulación de los valores
de una, o alguna, o todas las variables involucradas en nuestro modelo podemos
utilizar el icono
, cuyo uso es análogo al de
. Trate usted de llegar al siguiente resultado en tabla como lo indica la figura
8.
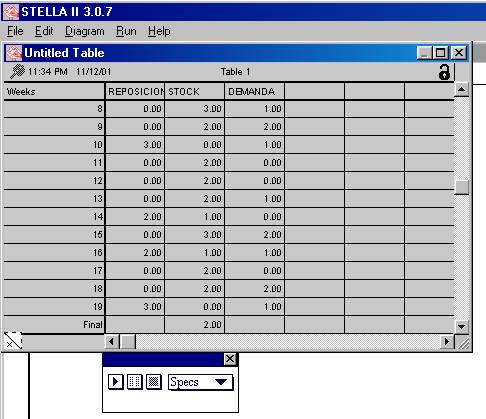
Figura 8