Supongamos que tenemos un lago de volumen constante, de manera que los flujos de entrada y salida son constantes, como se observa en la figura siguiente:

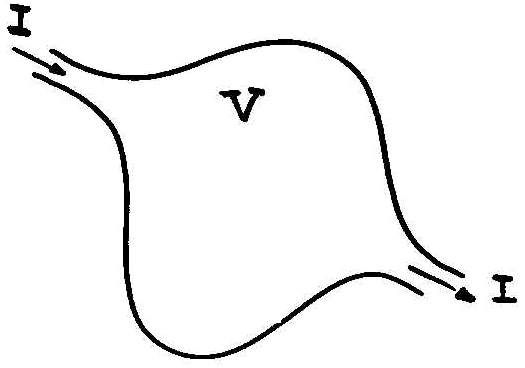
Supongamos que el lago ya se encuentra contaminado (alguien vertió polución desde una orilla del lago, por ejemplo), de manera que por el flujo de entrada solo fluye agua limpia, y es por el flujo de salida que sale agua contaminada. Vamos a suponer también, que la contaminación está distribuida homogéneamente por todo el lago, esto significa que todo punto del lago tiene la misma concentración de contaminante. Ahora bien, se desea estudiar la evolución dinámica de la concentración de contaminante en el lago con las hipótesis anteriores. Para esto, definamos las siguientes variables,

V = volumen del lago (metros cúbicos)

I = Flujo de entrada y salida del lago (metro cúbico por segundo)

P(t) = Volumen de polución en el tiempo t (metro cúbico)

y(t) = P(t) / V(t) = concentración de polución (adimensional)

Es claro que para este problema, la variables de estado es el volumen de contaminante, que irá disminuyendo a través del tiempo en virtud de que el lago ya está contaminado y que la contaminación fluirá por el flujo de salida. Ahora bien, es claro que el flujo de contaminante que sale del lago será porporcional al flujo de salida, y el factor de proporción es justamente la concentración de polución.

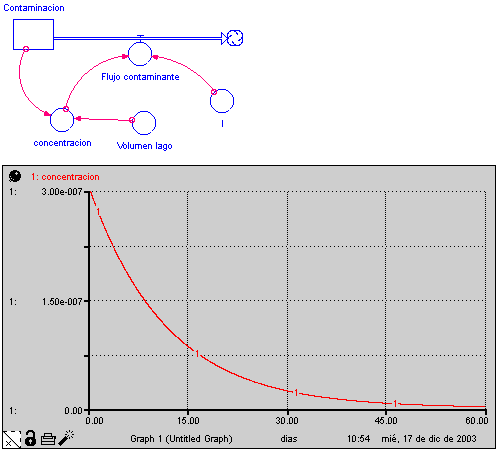
Consideremos los siguientes datos numéricos:

V = 10⁶ m³

I = 1 m³/ seg = 84600 m³/ día

P(0) = 3/10 m³

^{A continuación presentamos el Diagrama de Forrester del modelo, y la evolución de la concentración en función del tiempo:}

Para bajar el modelo en ambiente STELLA aquí

Un segundo modelo: Suponga que para el mismo lago no existe polución. Sin embargo por el flujo de entrada al lago empieza a entrar polución (por culpa del vertido de una industria río arriba, por ejemplo) a una razón de concentración dada por la función:

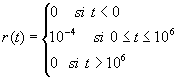
Es decir, esta vez existe flujo de alimentación (flujo de polución) para la variable de estado P(t). Se pide realizar un modelo en el ambiente STELLA para este problema.

Volver al menú principal