Modelos Deterministas de Epidemias
Eliseo Martínez H
En el modelamiento de la propagación de una epidemia es conveniente subdividir la población afectada por una epidemia en subpoblaciones básicas: susceptibles, incubadores, infecciosos, resistentes o inmunes, en período de latencia. Es importante considerar también los llamados portadores, que son los individuos que portan y transmiten la enfermedad aún cuando no presentan síntoma alguno. También en algunos casos conviene considerar los casos subclínicos, que son los individuos que realizan una enfermedad inaparente, es decir, sin presentar síntomas. En diversos modelos se suele introducir el concepto subpoblacional de removidos, que sirve para indicar un infecciosos que ha sido sacado de circulación por cuarentena, por haber terminado su período infeccioso o simplemente por muerte. Existen varias enfermedades importantes que no se transmiten directamente de un infeccioso a un susceptible, sino que lo hacen por medio de otro ser vivo (mosquito, amebas, roedores, etc.). Estos animales transmisores reciben el nombre de vectores. El estudio de tales enfermedades requerirá por tanto el análisis de dos poblaciones diferentes.
Muchas veces, más que el número de enfermos que hay en cada instante de tiempo, interesa conocer la llamada curva epidémica, que es la frecuencia con que ocurren nuevos casos. Y su definición matemática es relativamente sencilla. Supongamos que X(t) denota el número de infecciosos en el tiempo t, luego entonces X(t + Dt) - X(t) será el número de casos nuevos ocurridos en el intervalo [t, t + Dt], de manera que la curva endémica es
W(t) = lim tg0 W(t + Dt) - W(t) / Dt
Es decir, la curva endémica es la "velocidad" de la epidemia (número de enfermos por unidad de tiempo).
Se dice que un enfermedad es endémica, cuando se están constantemente presentando casos nuevos, sin que sea posible erradicarla totalmente. Por el contrario, se habla de brote epidémico cuando ocurre una fuerte incidencia de casos que terminan después de cierto tiempo. En estos casos es importante también el concepto de tamaño total de la epidemia, que es el número total de casos ocurridos durante todo el transcurso del brote. En los modelos matemáticos este tamaño total aparece generalmente en forma de límites cuando tg0.
Lo que haremos a continuación será de modelar conforme al lenguaje de Forrester los modelos clásicos matemáticos de epidemias determinísticas, que si bien estos están regulados por ecuaciones diferenciales para el neófito en matemática serán fácilmente accesibles (y una buena oportunidad para la interacción entre el especialista epidemiológico y el matemático)
La epidemia simple determinística
En este modelo la variable es estado es la población de infecciosos, y se considerará a la población total como constante, digamos N. Luego aparece la invariante de que el número de susceptibles más el número de enfermos es la población total. Además la hipótesis fundamental será de que el número de nuevos enfermos será proporcional a los que ya están enfermos y por el número de susceptibles en ese momento, esto es si Y(t) es el número de infecciosos en el instante t y X(t) es el número de susceptibles en el instante t entonces los infecciosos en el instante t + Dt está dada por
Y(t + Dt) = Y(t) + b Y(t) X(t) Dt (1)
donde b es una constante de proporcionalidad llamada constante de contagio. Y es claro que X(t) = N - Y(t) por la hipótesis de invarianza anterior. Buscando la ecuación diferencial, al dividir por Dt y buscar el límite cuando Dt g0, se llega a una ecuación tipo Ricatti:
Y´(t) = b Y(t) (N - Y(t))
suponiendo que se conoce el número de infecciosos en t = 0, esto es Y(0) conocido, y además siempre se cumple que 0 < Y(t) < N para todo t.
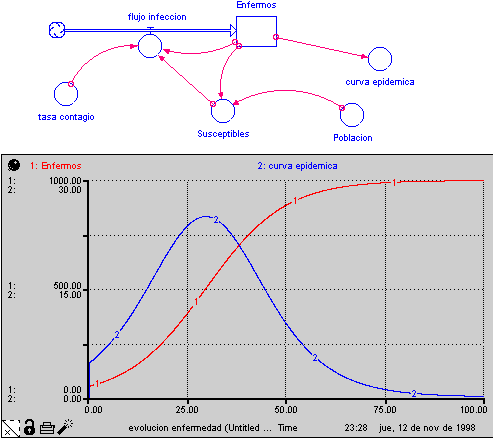
Con la ecuación dinámica en (1) estamos en condiciones de realizar un modelo tipo Forrester: la epidemia simple determinista. Aquí presentamos el Diagrama de Forrester, y la evolución de los enfermos así como la curva epidémica.

La epidemia general determinista.
En este caso la población se divide en tres subclases: en susceptibles, X(t); infecciosos, Y(t); y removidos Z(t) = N - X(t) - Y(t). El nivel de la población enferma se alimentará de los nuevos casos de contagio pero también habrá una disminución de este nivel al llevar a cuarentena algunos enfermos de modo que no puedan contagiar, en rigor se tienen las ecuaciones dinámicas:
Y(t + Dt) = Y(t) + b X(t) Y(t) - g Y(t) Dt
X(t + Dt) = X(t) - b X(t) Y(t) Dt (2)
Z(t + dt) = Z(t) + g Y(t) Dt
donde b representa la constante de contagio y g representa la tasa de removidos. Buscando las ecuaciones diferenciales al dividir por Dt y pasando al límite se obtiene el siguiente sistema de ecuaciones diferenciales
X´(t) = - b X(t) Y(t)
Y´(t) = b X(t) - g Y(t) (3)
Z´(t) = g Y(t)
con las condiciones iniciales: Y(0) = Y0 = número inicial de infecciosos; Z(0) = 0 = número inicial de removidos; X(0) = N - Y(0) = número inicial de susceptibles, y la condición "invariante": X(t) + Y(t) + Z(t) = N.
De la ecuación (3) se concluye que se desarrollará la epidemia si Y´(0) > 0, de lo contrario solo disminuirá el número de infecciosos al inicio de la epidemia en el tiempo; luego imponiendo esta condición, y reemplazándola en la segunda ecuación diferencial de (3) se tiene
(b X0 - g) Y0 > 0
y puesto que Y0 es positivo, se tiene que la condición de desarrollo de la epidemia es equivalente a
b X0 - g > 0 n X0 > g / b
La resolución analítica del sistema diferencial (3) no es soluble por funciones elementales. Ahora bien, las ecuaciones dinámicas dadas en (2) se pueden modelar fácilmente mediante la técnica de Forrester.