Eliseo Martínez
Se presenta una secuencia de mejoramiento de modelos que explican, en forma holística, la dinámica de una civilización que se inicia bajo un sistema de sociedad agrícola primitiva, logrando romper la maldición malthusiana, y que llega a una estabilidad a pesar de la revolución industrial que consiste en la creación de tecnología para la producción de sus alimentos (cf. Dynamic Modeling, Hannon B. y Ruth M., Springer-Verlag, pp. 32-45)
Modelo de Industrialización de una Sociedad Agraria Simple.
La situación a modelar: Consideremos una población inicial de personas en una cierta isla con una determinada área geográfica, de modo que por razones extrañas hay una cierta cantidad de comida escondida, siendo esta la única fuente de nutrición y, además, controla el nivel de la población. Los miembros más viejos de la población barruntan que la comida se acabará pronto, y proponen a la comunidad que diseñen un racionamiento, mientras ellos estudian la factibilidad de encontrar o crear alimentos suplementarios de forma continua. Después de algunos años descubren que el uso de herramientas en su proceso agrícola primitivo les facilitará la labor en el campo, y además lo hará más productivo. Entonces ellos fabrican herramientas, mediante la construcción de factorías que producen estos implementos para su agricultura, se producen cambios en las actividades laborales (gente para la agricultura, gente para las factorías)... comienza la formación de las grandes ciudades del mundo.
Metodología de trabajo: ¿Cómo es posible comenzar a modelar el proceso económico de la civilización hasta la revolución industrial? Aconsejamos que se comience desde lo simple y paulatinamente lo vayamos complicando. Una vez que las características básicas de la población agrícola sean capturadas en un modelo simple, podemos refinar el modelo y extenderlo para incluir el proceso de la creación de alimentos y la construcción de herramientas.
El primer modelo: Vamos a considerar dos variables de nivel, la población y los alimentos (unidades, personas y kilos respectivamente). Supongamos que los valores iniciales para la población y los alimentos son 10 personas y 1000 kilogramos, respectivamente. La población es regulada por dos flujos, uno de entrada, número de personas que nacen por unidad de tiempo, y uno de salida, número de personas que mueren por unidad de tiempo. Al flujo de entrada le llamaremos flujo de nacimiento, y al flujo de salida flujo de muerte. Vamos a suponer que el flujo de nacimiento está controlado por una variable llamada razón de nacimiento. La unidad de esta razón de nacimiento es importante y no podemos soslayarla: nuevas personas que nacen por personas que están en la población, por unidad de tiempo; (a estas alturas digamos que la unidad de tiempo es el año). Supongamos que la razón de nacimiento es función de la densidad de población, esto es número de habitantes por área geográfica, ahora si suponemos que el área de nuestra isla es de 1 (si es preciso la normalizamos), entonces con cierto abuso de lenguaje podemos decir que la razón de nacimiento es función de la población. Estudios antropológicos nos dicen que cuando hay suficiente espacio la razón de nacimiento alcanza su máximo valor de 0.1, y que el máximo permisible de habitantes para la isla es de 200 personas, lo que significa que necesariamente la razón de nacimiento debe ser (o estar próxima) a cero para esta densidad. En definitiva los estudiosos nos entregan el siguiente cuadro:
Población Razón de nacimiento
2.00 |
0.0995 |
21.8 |
0.0975 |
41.6 |
0.091 |
61.4 |
0.0885 |
81.2 |
0.083 |
101 |
0.075 |
121 |
0.062 |
141 |
0.053 |
160 |
0.035 |
180 |
0.015 |
200 |
0 |
El flujo de nacimiento necesitará de esta razón de nacimiento, y además necesitará el nivel de la población para cada año, de otra forma este flujo de nacimiento (de un determinado año) es igual a la razón de nacimiento por la población (de ese año).
Por otro lado, el flujo de muerte depende de una razón de muerte (cuya unidad es personas muertas por personas de la población, por año), y de la población, pero por estudios que se han hecho se sabe que la razón de muerte es función de la comida per capita (kilogramos por persona), a su vez por razones de racionamiento, puesto que la comida en esta sociedad primitiva es finita, esta comida per capita es función de la alimentación per capita. Las relaciones anteriores se entregan en los siguientes cuadros
Comida per capita Razón de muerte
0.00 |
0.187 |
0.1 |
0.19 |
0.2 |
0.184 |
0.3 |
0.173 |
0.4 |
0.163 |
0.5 |
0.147 |
0.6 |
0.121 |
0.7 |
0.095 |
0.8 |
0.061 |
0.9 |
0.028 |
1.0 |
0.013 |
Alimentación per capita Comida per capita
0.00 |
0.00 |
1.0 |
0.04 |
2.0 |
0.155 |
3.0 |
0.27 |
4.0 |
0.385 |
5.0 |
0.52 |
6.0 |
0.63 |
7.0 |
0.72 |
8.0 |
0.82 |
9.0 |
0.92 |
10.0 |
0.995 |
El diagrama de Forrester de este sistema, las ecuaciones dinámicas y una simulación se pueden observar haciendo click aquí.
Un segundo modelo mejorado: Agregando la agricultura. Esto significa que entra un flujo de producción de alimentos sobre la variable de nivel alimentos, y esta variable se regulará por el nivel de la población (más exactamente por la población laboralmente activa), y por un par de coeficientes tecnológicos. El grupo de economistas de la isla concluye tímidamente que la variable de flujo producción de alimentos se rige por:
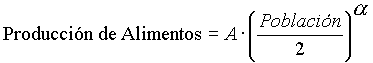
El nuevo diagrama de Forrester para este modelo, las ecuaciones dinámicas y una simulación se puede observar haciendo click aquí.
Un tercer modelo mejorado: Agregando la industria. A la luz de los resultados anteriores y a objeto de evitar la maldición Malthusiana introducimos la industria en esta sociedad primitiva, que se reflejará en la variable de nivel implementos, que servirán para mejorar la producción agrícola. Esta variable es regulada por dos flujos, el de salida llamado depreciación (vamos a suponer una depreciación constante de 0.04 por cada implemento), y el de entrada llamado manufacturación que es regulado por la población laboral dedicada a las fabricas y un par de coeficientes tecnológicos. Se propone:
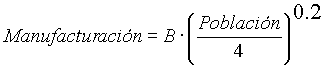
de manera que la (nueva) variable producción de alimentos queda como:
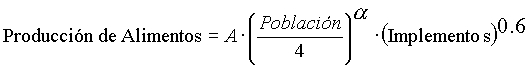
El diagrama de Forrester para este modelo y su evolución en el tiempo se puede observar haciendo click aquí.