|
Dinámica de población: un modelo
mejorado |
| |
| En nuestro modelo anterior parece
haber una "linealidad" o sencillez que perturba. En efecto, si
consideramos que la población de Antofagasta, bajo nuestro primer
modelo, en 10 años más tendrá 613273, es decir de un crecimiento de
613273 - 547933 = 65340
habitantes respecto de la población del año 2006.
No parece real que se
mantenga el mismo número de nacimientos, puesto que si hay más población
parece natural pensar que habrá mas matrimonios y en consecuencias más
hijos. De la misma forma, si aumenta la población es indudable que haya
un número mayor de fallecidos anualmente respecto de la cifra constante
del flujo de mortandad de nuestro primer modelo. |
| Bajo este predicado, de que a mayor
población mayor nacimiento y mayor número de fallecidos, debemos
modificar nuestro primer modelo, podemos concluir que los flujos de
nacimientos y muertes dependerá, de alguna forma, del propio nivel
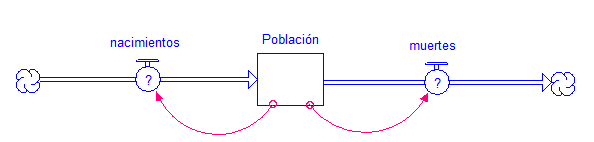
poblacional que haya en ese momento. Observemos la siguiente figura |
| |
|
 |
|
Figura 1 |
| |
|
Es decir, hemos trazado sendos
conectores desde la variable de estado Población hacia los dos flujos.
Ahora bien, la pregunta es ¿el valor de los flujos se desprende
solamente del valor de la Población? |
| Una parte de la población, al año,
puede crear nacimientos, por ejemplo, si elegimos al azar mil personas
¿cuántos nacimientos pueden ocurrir? Quizá nos puede ayudar en esta
línea la biología celular: Se sabe que una célula se particiona, en un
determinado tiempo, de modo que si hay 4 células al cabo de ese
determinado tiempo habrá 8 células, y después 16, y así sucesivamente.
Se resume este fenómeno diciendo que la tasa de nacimiento celular es de
2 células nuevas sobre cada célula. Sin embargo, la población humana no tiene esa
propiedad de que cada persona genere otra persona por sí sola, piense
usted que de 3 personas no hay seguridad que alguna de ellas genere un
nacimiento. Sin embargo podemos hacer una estimación basada en la
estadística, y existen procedimientos para estimar el promedio de recién
nacidos por cada mil personas. A este valor se le llama tasa de
nacimiento. A modo de ejemplo, supongamos que en Chile, por cada mil personas hay 25
nacimientos anuales, estimativamente. De esta manera, la
tasa de
nacimiento en Chile, en promedio, es de 25/1000 = 0,025. Y esto
significa que de cada 2000 personas habrán 50 nuevos nacimientos
anuales, y de cada 3000 personas habrán entonces 75 nacimientos anuales.
De tal forma que si la población de Antofagasta es X habitantes en un
determinado año, entonces en ese año se espera estimativamente unos
0,0025*X nacimientos. |
| Un razonamiento similar nos permite
definir la tasa de mortandad, esto es el valor estimativo del número de
fallecidos por cada 1000 personas. Supongamos que este valor para Chile
es de 11 por cada 1000 personas, de modo que la tasa de mortandad es de
11/1000 = 0,011. |
| |
| Nota: cuando decimos de que por cada
1000 personas hay 25 personas que nacen al año, decimos entonces que el
valor numérico de la tasa, 0,025, tiene las unidad de 1 / año (unidad de
frecuencia), o con más naturalidad la tasa de nacimiento se expresa como
0,025 personas nacidas vivas / personas * año |
| |
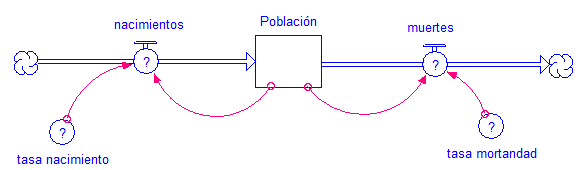
| Observemos entonces la siguiente figura, |
|
 |
|
Figura 2 |
|
Ahora, como lo enseñamos, hacemos
click en cada variable con el signo "?" y entregamos ya sea su valor,
como es el caso de las tasas, o ya sea su dependencia analítica como es
el caso de los flujos. |
|
|
|
 |
|
Figura 3 |
| |
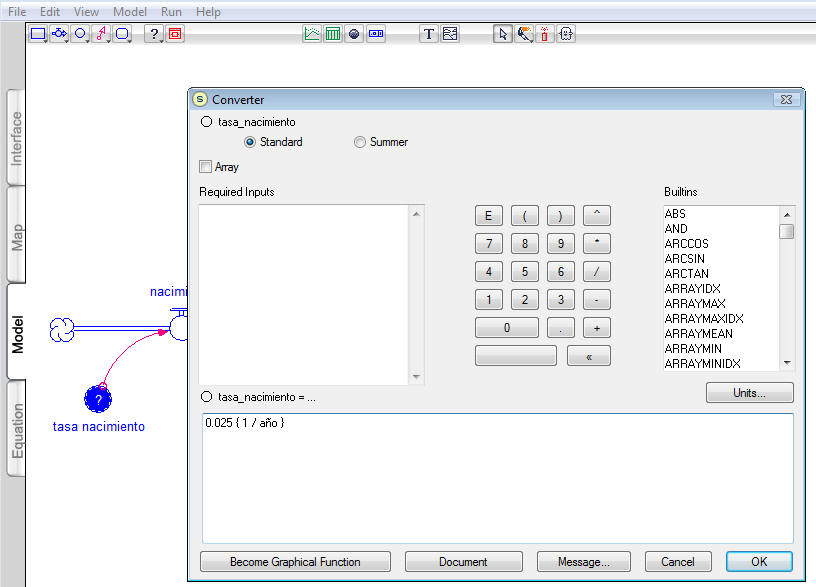
| Hacemos click ahora en "tasa de nacimiento" y entregamos su valor de
0,025. Esto es, |
| |
|
 |
|
Figura 4 |
| |
| Con las otras variables actuamos de manera similar,
de modo que estamos en condiciones de hacer "correr" nuestro modelo. |
| |
|
 |
|
Figura 5 |
| |
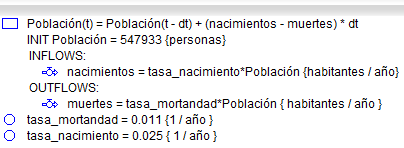
| Si hacemos click en la pestaña "Equation" obtenemos, |
| |
|
 |
|
Tabla 1 |
| |
|
Vamos a estudiar la evolución de la
población de Antofagasta, durante 101 años, esto es desde 2006 hasta el
2106, mediante un gráfico, pero esta vez subiremos a la "cabina de
vuelo". Hagamos click en la pestaña "Interface" |
| |
|
 |
|
Figura 6 |
| |
|
En esta área de "Interface" pinchamos
un gráfico asegurándonos de fijarlo con la chincheta y luego elegimos la
variable a describir que será la Población, esto es |
| |
|
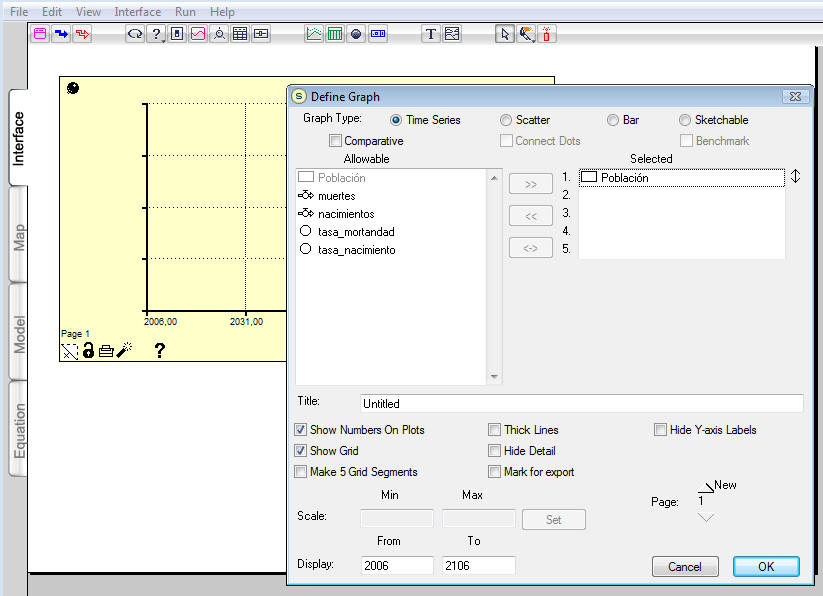 |
|
Figura 7 |
| |
| Luego de seleccionar a la variable Población,
volvemos al área Interface y seleccionamos el menú run seguido de run
spec... para determinar la longitud de tiempo y el valor de DT, observe
la Figura 8 |
| |
|
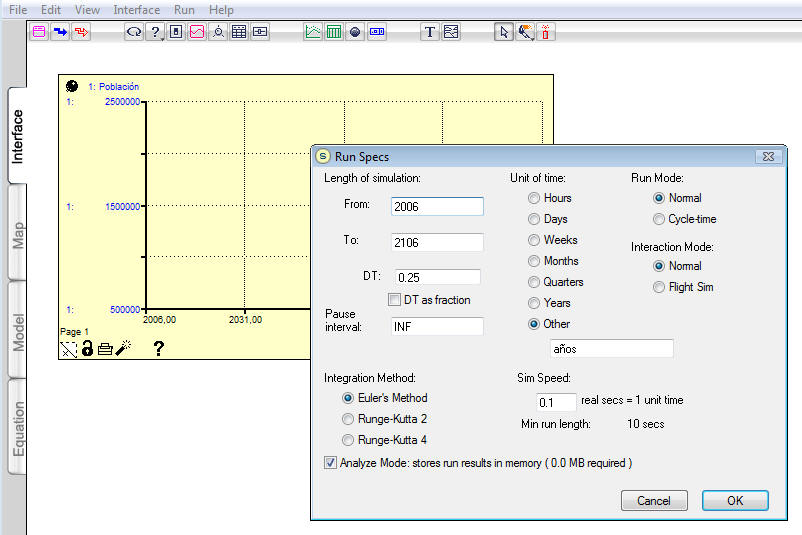 |
|
Figura 8 |
| |
| El valor de DT = 0,25, y puesto que la unidad de
tiempo es el año, significa que el modelo nos estará entregando
resultados cada cuarto de año, esto es cada trimestre. Luego hacemos
correr el modelo y obtenemos, |
| |
|
 |
|
Gráfico 1 |
| |
| El Gráfico 1 nos dice que el año 2081, o sea en 86
años más a partir del 2006 que contaba con 547933 personas, habrán más
de un millón y medio de personas. |
| Usted, entonces, ¡tiene capacidad para predecir el
futuro de acuerdo a este modelo! |
| |
|
Preguntas a este modelo |
|
|
| 1. ¿Le satisface este modelo para explicar la
dinámica de la población de Antofagasta? |
| 2. ¿Según este modelo, cuánta gente tendrá
Antofagasta en el año 2500? |
| 3. ¿La población de Antofagasta crecerá
indefinidamente hasta el fin de los siglos? |
| |
|
Volver a la página principal |









