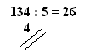|
Dirigidos a los profesores del programa de postítulo en la especialidad de matemáticas |
| Instructor: Dr. Eliseo Martínez Herrera |
| Tema de la clase: Ayudar a descubrir el algoritmo de la división mediante el uso adecuado de la calculadora. |
| Objetivo de la clase: Se promueve el uso de la calculadora tanto para resolver operaciones que requieren de cálculos (en ocasiones largos y tediosos, que pueden distraer la atención de aspectos centrales del problema que se desea resolver), como para facilitar la investigación de regularidades numéricas. En particular utilizaremos la calculadora para reforzar el algoritmo de la división en esta ocasión. |
| Desarrollo de la clase: Suponemos que la "operación de la división" la entiende el alumno como la distribución de una cantidad de objetos (naranjas) en una cantidad de sectores (canasta), y los objetos que no alcancen a distribuirse en los sectores (canastas) constituyen el "resto", y este resto no debe superar el número de sectores. Lo fundamental, entonces, para realizar una división es saber multiplicar y determinar el resto adecuado. |
| Vamos a empezar con el siguiente ejercicio: |
|
134 : 5 |
| insistiendo, hasta el cansancio, que esta expresión significa que 134 objetos se quieren distribuir en 5 cajas o sectores, o agrupamientos, de tal forma que los objetos que no puedan distribuirse serán menores que 5 (0, 1, 2, 3, 4). ¿Cómo empezamos a agrupar?. |
| Preguntamos, ¿con cuantos objetos podemos empezar a repartir en estos 5 sectores? Tendremos una diversidad de respuestas, por ejemplo 10, 25, 30, etcétera. Observemos que la siguiente tabla se puede "ejecutar" |
|
Tabla 1 |
| Esta tabla indica un procedimiento para ejecutar el algoritmo de la división. En la columna que hemos llamado "Propongo", indica que un alumno empezará a repartir de 20 en 20, hasta llegar a los 5 grupos. Ahora bien, para saber lo que alcanza a distribuir en los 5 grupos es simplemente el producto |
|
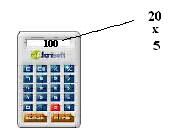
20 x 5 = 100 |
| Le pedimos al alumno que saque su calculadora. El alumno lo ejecutará con la calculadora, esto es |
|
|
| Y este resultado lo pondrá en una segunda columna, que hemos llamado "Producto", y que calcula el número total de objetos que hemos logrado repartir de 20 en 20. Luego en la tercera columna, que hemos llamado "Resto" escribimos el número de objetos que no se han podido repartir de 20 en 20, y que es la diferencia entre 134 - 100 = 34. De esta forma tenemos la primera fila de nuestra tabla con los valores 20 5 34, como se indica en la Tabla 1. |
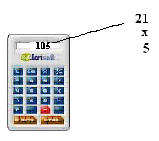
| Ahora bien, puesto que el 20 no satisface la "mejor distribución" toda vez que el resto nos da 34, que es mayor que 5, incrementamos en 1 el valor inicial de 20. Luego con el 21 realizamos la misma operación, esto es, |
|
|
| Ponemos el 21 en la columna de "Propongo", luego en la columna "Producto" ponemos el 105, y luego calculamos el resto, que es 29. |
| Realizando iteradamente estos cálculos llegaremos al final de la fila, dada por 26 5 4, que nos indica que se distribuyen 26 objetos en 5 sectores y sobran 4 objetos. Es decir, hemos calculado la división, y la escribimos como |
|
|
| Observemos que en este desarrollo aparece la siguiente regularidad (la columna "Propongo" se incrementa en una unidad, la columna "Producto" se incrementa en 5 unidades, y la columna "Resto" disminuye en 5 unidades") |
|
|
| Es posible que alguien proponga lo siguiente: empezar con 30, lo cual se obtiene por la calculadora que 30 x 5 = 150, y esto significa que nos "pasamos" en la forma de distribuir, no obstante podemos realizar una tabla similar como la que se indica a continuación |
|
|
| Puesto que nos pasamos podemos ir decreciendo en una unidad (esto es una opción, el alumno puede tantear con una disminución más rápida). De igual forma es útil hacer ver la nueva regularidad que aparece en esta tabla. En la columna "Propongo" se disminuye en una unidad, y en la columna "Producto" se disminuye en 5 unidades respectivamente, puesto que claramente los sucesivos restos serán negativos, no los ubicamos en la columna "Resto", excepto a aquel primero que nos satisface. |
| Rigurosamente hablando, este "tanteo" es similar al clásico algoritmo de la división. |
| Realicemos el siguiente ejercicio, |
|
1457 : 3 |
| Una posible trayectoria de solución es la se muestra a continuación: |
|
|
| Algunas consideraciones: Pida al alumno que realice la siguiente división (sin calculadora, y aún cuando no haya memorizado las tablas de multiplicar): |
|
22: 3 |
| Si el alumno se sabe la tabla de multiplicar, con seguridad buscará cuál es el producto de la tabla del 7 que más se aproxima al 22 por abajo, y este es el 7 x 3 = 21, de modo que el "resto" es 1, en consecuencia el resultado es 7 y sobra 1. |
| Ahora si el alumno no se ha aprendido aún la tabla del 7, pídale que complete la siguiente tabla e indíquele que puede usar la calculadora, |
|
|
| De esta manera reforzamos la necesidad de que para divisiones fáciles, esto es cuando hay que "distribuir" objetos que no superen las centena, es muy fácil si nos sabemos la tabla de multiplicar, y para distribuir cantidades muy grandes, es mejor usar la calculadora. |