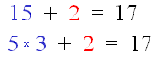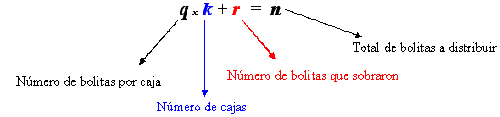|
Dirigidos a los profesores del programa de postítulo en la especialidad de matemáticas |
| Instructor: Dr. Eliseo Martínez Herrera |
| Tema de la clase: División mediante distribución en partes iguales con resto. |
| Objetivo de la clase: Enseñar a distribuir una serie de objetos del mismo tipo en partes iguales permitiendo que sobren objetos. |
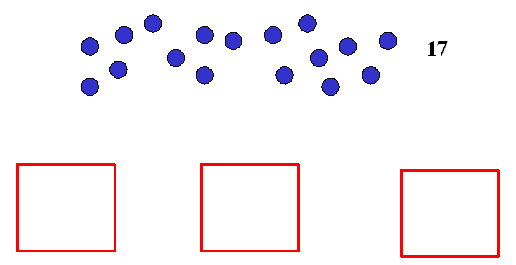
| Desarrollo de la clase: Se presentarán tres cuadrados donde se deberá deposita el máximo de objetos de tal forma que cada cuadrado contenga el mismo número de objetos. El número de objetos a distribuir no será múltiplo del número de cuadrados, de tal forma que el alumno entienda el concepto de "resto" o "sobra" de una distribución equitativa. Se presentará el siguiente cuadro: |
|
|
| Se pedirá a los alumnos y alumnas lo siguiente: Distribuir las bolitas azules en partes iguales entre los tres cuadrados rojos. |
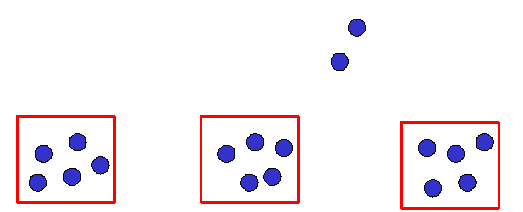
| Se supone que estos alumnos y alumnas no asociarán este problema a resolverlo mediante el proceso de la multiplicación, de manera que se espera que empiecen la distribución de una bolita por cada caja, hasta ir agotando el stock de bolitas azules. El problema emergente será que al alumno y alumna le sobrarán dos bolitas. Deban reconocer esta situación como la que es: "sobraron dos bolitas". |
|
|
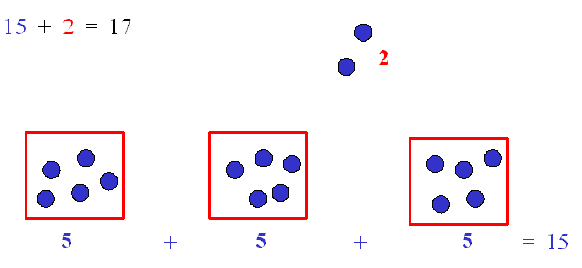
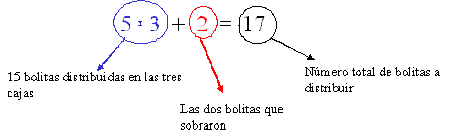
| Se les pedirá ahora si entre el total de bolitas distribuidas y las que sobraron, efectivamente "hacen" las 17 bolitas originales. Los alumnos deberían concluir de la siguiente manera: |
|
|
| La parte crucial ahora, es que puedan reconocer el siguiente desarrollo: |
|
|
|
|
|
|
| Los estudiantes descubrirán (si no es así, reforzamos esta conclusión marcando en la pizarra el número 5 de las bolitas en cada caja y el número de cada caja) que el número 3 está asociado al número de cajas y el número 5 al número máximo de bolitas que se pudo repartir en cada caja. |
| Ahora replicamos el problema pero esta vez trabajaremos con 19 bolitas. Los estudiantes pueden nuevamente hacer la distribución de las bolitas en cada caja de uno en uno (si no es así, no importa), pero deberán concluir que se distribuirán 6 bolitas por caja y sobrará una bolita, esto es |
|
6 x 3 + 1 = 19 |
| Deberán reconocer el papel que juega el número 6 (número de bolitas por cada caja) y el 3 como el número de cajas, y les sobra una bolita. |
| Ahora viene el problema abierto: ¿En qué caso no sobrará ninguna bolita? |
| Como alternativa se puede realizar un problema esta vez con un número de bolitas que sea múltiplo al número de cajas. En cualquier caso no estemos tentados a definir todavía el "algoritmo de la división". Esto deberá concluirse en una próxima sesión. |
| Se deben continuar con ejercicios sencillos de tal forma de reforzar la siguiente conclusión |
|
|
|
|
| Material didáctico a usar: Bolitas azules de goma pegadas con cinta adhesiva doble. Las cajas o cuadrados se dibujan en el pizarrón con tiza roja. |