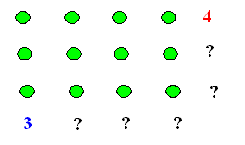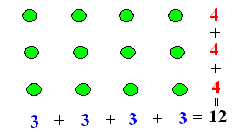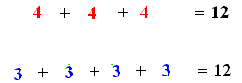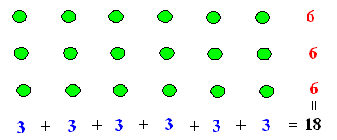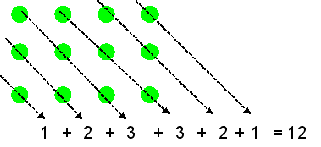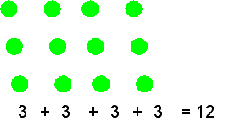|
Dirigidos a los profesores del programa de postítulo en la especialidad de matemáticas |
| Instructor: Dr. Eliseo Martínez Herrera |
| Tema de la clase: Multiplicación mediante arreglos rectangulares |
| Objetivo de la clase: Utilizaremos los arreglos rectangulares como modelo didáctico para la enseñanza de la multiplicación. Con este modelo didáctico, creemos que será natural la comprensión del concepto de multiplicación entre dos números, así como la conmutatividad en la multiplicación. Con este modelo, creemos, no se hará extremadamente necesario el aprendizaje de memoria de las tablas de multiplicar. Para la presentación de este modelo didáctico utilizaremos la técnica metodológica de "problemas abiertos". Con este modelo didáctico definiremos de manera natural que le expresión ab tiene dos significados iguales, que es a veces el número b, y es b veces el número a. |
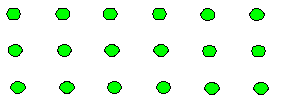
| Desarrollo de la clase: Se presentará el siguiente arreglo rectangular |
|
|
| Y se les preguntará a los alumnos ¿cuántas pelotitas verdes hay en este dibujo? |
| Esperamos los siguientes resultados. Los estudiantes contarán las pelotitas, y es altamente probable que las cuenten desde derecha a izquierda y desde arriba hacia abajo. Esperaremos un tiempo prudente para este conteo, pediremos que levanten la mano quien tiene el resultado, elegiremos a un alumno y conforme sea cual sea su respuesta, diremos ¿cómo lo calculó? |
| Si es que el alumno simplemente ha contabilizado mediante el conteo que hemos supuesto (hacia la derecha y desde arriba hacia abajo), cuyo resultado debiera ser 12, haríamos la siguiente pregunta al curso, ¿alguien ha contado de otra forma? |
| Si no hay respuesta en cuanto a otra metodología a contar, diremos lo siguiente: cuenten, por favor, desde arriba hacia abajo y desde la derecha hacia la izquierda, y luego reforzamos el cálculo mediante la pregunta ¿obtuvimos el mismo resultado? (Nota: es posible que algunos alumnos o alumnas inventen otro método de conteo, como por ejemplo a través de las diagonales de este arreglo, lo cuál habría que aceptar el reto y no desechar esta opción, observe la figura del anexo) |
| Sobre el mismo dibujo, el profesor agrega los siguientes números y signos, conforme lo indica la figura siguiente |
|
|
| El profesor pregunta al curso, ¿qué números debemos poner donde aparecen los signos de interrogación? Esperando las respuestas correctas (estando muy atento a las incorrectas y sin DESPRECIAR ni INHIBIR las incorrectas), agregamos la siguiente pregunta, ¿porqué han dado esa respuesta? o de otra forma, ¿porqué hemos puesto el número 3 en las "columnas", y en las "filas" el número 4? |
|
|
| Los alumnos deberán ellos mismos comprender (que el profesor no esté tentado a "descifrar" el resultado) de que esos números determinan el número de pelotitas que hay tanto por fila (4), y el número de pelotitas que hay por columnas (3). Hay que estar atento a las diferentes redacciones que entregarán los niños y niñas. Estas pueden ser: el número de pelotitas que "aparecen en las líneas horizontales" , el número de pelotitas en las "rayas horizontales", etcétera. Si hay varias redacciones para el mismo hecho los alumnos deberán anotar en su cuaderno estas interpretaciones (cuidando el profesor que no haya ambigüedad en alguna de ellas). |
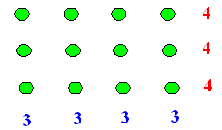
| El profesor hará ahora la siguiente pregunta: ¿Observan alguna relaciones entre los "3" y los "4"?. |
|
|
| El profesor deberá estar atento a la avalancha de respuestas, sin inhibir ninguna, dirigirá la discusión de que hay tantos "3" como lo indica el número 4, y viceversa. Y enseguida preguntará, ¿cómo puedo, entonces, contar el número de pelotitas? |
| Al escuchar las respuestas de los alumnos, con toda seguridad quedará resumida en el siguiente gráfico: |
|
|
|
El profesor, puede reforzar estos resultados mediante la siguiente secuencia de preguntas: ¿cuántas pelotitas hay por en cada fila?, ¿cuántas filas hay? ¿cuántas pelotitas entonces hay en ese dibujo? |
|
Y las preguntas alternativas: ¿cuántas pelotitas hay por cada columna?, ¿cuántas columnas hay? ¿cuántas pelotitas entonces hay en ese dibujo? |
|
Actividad alternativa |
|
A continuación viene el desafío si el alumno es capaz de transportar un modelo conocido a un modelo reciente (el de los grafos bipartitos a este modelo de arreglos rectangulares): |
|
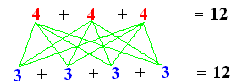
Diremos al alumno: Puesto que ya sabemos la cantidad de pelotitas verdes que hay en este dibujo, reubiquemos los números "4" y los números "3" de la siguiente forma: |
|
|
| Se les preguntará. ¿les recuerda algo este sistema de conteo? En la espera de esta respuesta le pedimos a los alumnos que revisen el cuaderno con la clase anterior. Creemos que varios alumnos responderán con la siguiente construcción |
|
|
|
|
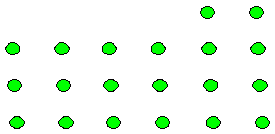
| A continuación planteamos el siguiente problema: Sin contar las pelotitas de una en una ¿cuántas pelotitas hay en el siguiente dibujo? |
|
|
| El alumno o alumna debería concluir lo siguiente: |
|
|
| En atención a los dibujos, le pedimos al alumno que
dibuje un esquema similar con 5 filas y 4 columnas, y a este
dibujo le llamamos 5*4,
indicando que hay cinco filas con 4 bolitas cada una, o, que es lo mismo,
cuatro columnas con cinco bolitas cada uno. Una manera de reforzar esta
regularidad es indicarle que dibuje un esquema de cuatro filas y cinco
columnas. |
|
Ahora se trata de continuar buscando las regularidades para que el alumno fije la multiplicación. El profesor puede establecer el siguiente ejercicio ¿Cuántas bolitas hay en una tabla de 3 por 5? (cambiamos la palabra dibujo o esquema por tabla con mucha naturalidad, sin explicar lo que es una tabla). Los alumnos, posiblemente preguntarán qué número indica la fila y qué número indica la columna? La respuesta del profesor debería ser: "Usted mismo decida cuáles son las filas y cuáles son las columnas". Se deberían tener los dos siguientes resultados en el curso: |
|
|
| Que el alumno construya la tabla del tres por uno, tres por dos, tres por tres, tres por cuatro, etcétera, hasta la tabla del tres por diez y bajo cada tabla registre el número de bolitas que contiene la tabla. |
| Planteemos el siguiente problema, y esperemos las respuestas para reforzar lo aprendido en clases: ¿De cuántas maneras divertidas se pueden contar las pelotitas que hay en el siguiente esquema utilizando las tablas? |
|
|
|
Anexo |
|
|
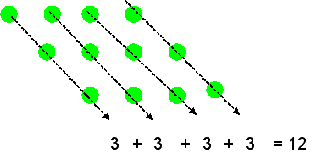
| Si un estudiante responde de esta manera, usted puede indicar lo siguiente ¿que tal si las bolitas que están solitas las ponemos en los lugares (diagonales) que tienen dos bolitas? |
|
|
| Material didáctico a usar: Las pelotitas de color verde se construirán con papel o esponja, adheridos al pizarrón. Los números para la suma a través de filas con tiza roja, y los números para indicar la suma a través de las columnas con tiza azul. |