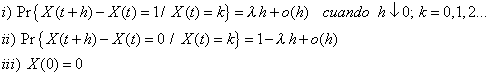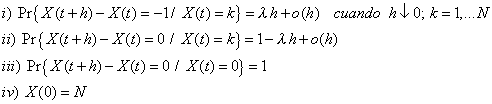| El proceso de Poisson es un proceso Markoviano que cumple los siguientes postulados |
|
|
|
El postulado (i) tiene una fácil interpretación en la teoría de la confiabilidad. En efecto, suponga que X(t) denota el número de elementos que fallan en el tiempo t, entonces la expresión |
|
|
| y la expresión de la izquierda es equivalente a la definición de función de riesgo. De modo que en este caso, el "riesgo" es constante y vale l. |
| Otra adecuación de este proceso, que llamaremos proceso de falla Poisson, es considerar que X(0) = N, y X(t) denota el número de componentes de un sistema que funcionan, donde las componentes son independientes e igualmente distribuidas, entonces un modelo de falla que se adecue a este proceso debe satisfacer lo siguiente: |
|
|
| No resulta complicado demostrar que, para el proceso de Poisson general, las probabilidades |
|
|
| vienen dadas por |
|
|
| Estos procesos son bastante adecuados para modelar sistemas con N componentes y donde la razón de falla se rige por una distribución de Poisson de parámetro l. |
| Para el caso del proceso de falla Poisson, es de interés el cálculo de P0(t). Es decir, la probabilidad de que en el tiempo t el sistema colapse completamente. Ahora, si T es el tiempo en que las N componentes del sistema falla, ¿cuál es E[ T ] ? Estas preguntas se dejan al alumno (o para una prueba). |