| En este tiempo, en virtud del desarrollo de los computadores, son accesibles una serie de estadísticos para realizar la dócima de hipótesis si una determinada distribución se ajusta o no a los datos. Estos estadísticos para la docima, aproximadamente unos 30 años atrás, pertenecían al campo de la "estadística avanzada" toda vez que su aplicación real y de poca frecuencia era costosa, puesto que el computador, como se conocía el computador entonces hace treinta años atrás, solo era accesible a los investigadores que contaban con los medios para su utilización. De manera que el estudio de tal o cual estadístico para la dócima de hipótesis de ajuste de distribución, tenía importancia para el estadístico matemático desde el punto de vista teórico. En la actualidad, resulta imprudente sistematizar la enseñanza teórica de una "técnica de ajuste" a una determinada distribución en un curso de Análisis de Confiabilidad, toda vez que la utilización de tal o cual "ajuste" está ampliamente difundida en cualquier paquete o software estadístico. Con esto no se quiere decir que el estudiante de las matemática estadística no debe saber los fundamentos y principios teóricos de estos, sin embargo, en la distribución del tiempo de enseñanza aprendizaje, digamos con más precisión, enseñar los fundamentos teóricos de los diez o más "pruebas de ajuste" que trae consigo cualquier paquete estadístico, no permitirá, paradójicamente, la aplicación de la teoría de la estadística matemática en lo que respecta al uso del Análisis de Confiabilidad. Con esto queremos decir que los métodos de ajuste de distribución lo confiaremos simplemente al área de estudio de la Estadística Inferencial. A modo de ejemplo, vamos a mostrar una simple página del Statgraphics en que resuelve un problema de ajuste, que perfectamente podría llevarnos unas cuatro horas en la justificación matemática de todas las pruebas o dócimas utilizadas para tal ajuste. |
| Se tienen los siguientes datos de tiempos de fallas de un determinado artículo electrónico medido en horas: |
|
|
| Vamos a docimar si estos datos se ajustan a una distribución exponencial, utilizando el software Statgraphics. Se muestran los resultados de salida: |
|
Resumen del
Análisis Dado que p-valor más
pequeño
de los tests realizados es superior o igual a
0.10,
no podemos rechazar que Tiempo fallas proceda de una
distribución exponencial con un nivel de confianza de al menos
un
90%. |
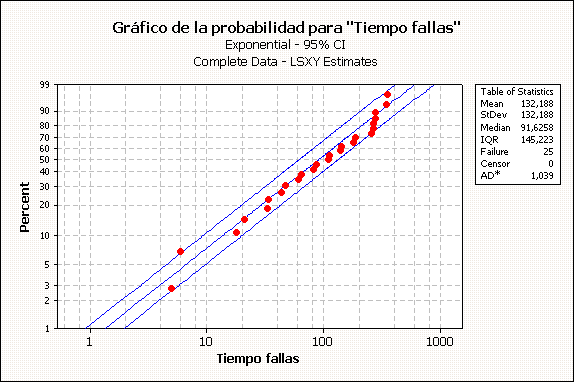
| Un análisis gráfico de ajuste a una exponencial para los mismos datos, esta vez en el software MINITAB, nos entrega el siguiente resultado: |
|
|
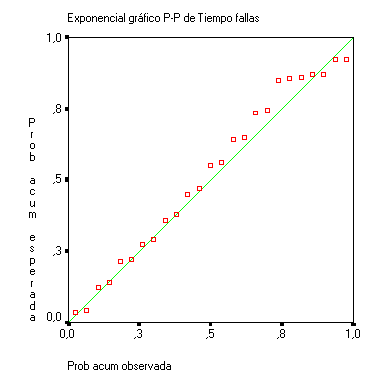
| Y para un ajuste a una exponencial, mediante la técnica P-P en el software SPSS, tenemos el siguiente resultado. |
|
Distribución contrastada:
Exponencial Fórmula de estimación de la proporción utilizada: Blom Rango asignado a empates: Media Para variable TIEMPO_F ... Parámetro de la distribución exponencial estimado: escala = ,00726744
|
| No deja de ser curioso que estos tres paquetes, que sin duda son los más frecuentemente utilizados, aplican diferentes técnicas de ajuste. |
| Dejaremos, por lo menos en este curso de confiabilidad, que las técnicas de ajuste sean vistas en un curso de estadística Inferencial, nosotros simplemente haremos la exigencia de utilizarlas correctamente. |
|
|