En lo que sigue, conforme sus cálculos oprima la tecla que se adecúa a su resultado. Sin embargo oprima cuando estè seguro, recuerde que un intento fallido descuenta puntaje.

1. La transformación lineal en las bases canónicas de la matriz es

   1.   ?    
   2.   ?    
   3.   ?    
   4.   ?    
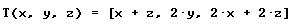
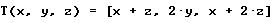
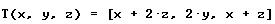
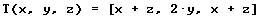
   5.   ?    Ninguna de las anteriores

2. El polinomio característico de la matriz es

   1.   ?    
   2.   ?    
   3.   ?    
   4.   ?    
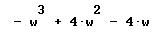
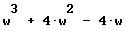
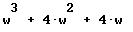
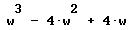
   5.   ?    Ninguna de las anteriores

3. Los autovalores de la matriz son

   1.   ?    -2 y 2
   2.   ?    los tres son valores complejos
   3.   ?    0 y -2
   4.   ?    0 y 2
   5.   ?    2, un complejo y su conjugado

4. Respecto de matriz cuales de los siguientes pares de vectores son autovectores de esa matriz:

   1.   ?    (2, 2, 2) y (3, 0 , 3)
   2.   ?    (2, 1, -2) y (3, 0, -3)
   3.   ?    (2, 1, 2) y (3, 0, -3)
   4.   ?    (1, 1, 1) y (3, 0, -3)
   5.   ?    Ninguno de los anteriores

5. Para la siguiente transformación lineal 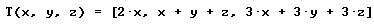el Kernel de T , Ker T, es

   1.   ?    Ker T = {<0, 3, 3>}
   2.   ?    Ker T = < (0, 0, 0) >
   3.   ?    Ker T = < (-3, 3, 1 )>
   4.   ?    Ker T = {<0, 1, -1>}
   5.   ?    Ninguna de las anteriores

6. La matriz asociada a la Transformación Lineal en las bases canónicas es

   1.   ?    
   2.   ?    
   3.   ?    
   4.   ?    
   5.   ?    Ninguna de las anteriores

7. El producto interior más frecuente en el espacio tridimensional, y que a veces se le conoce como producto punto en Física, es como sigue: 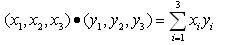. En relación a este producto interior la norma del vector (-3, -4, 0) es

   1.   ?    -3
   2.   ?    3
   3.   ?    2
   4.   ?    -5
   5.   ?    Ninguna de las anteriores

8. Para el mismo producto anterior sea v = (2, 3, 1), entonces el vector v multiplicado por el valor inverso de la norma de v vale:

   1.   ?    -2
   2.   ?    (2/3, 1, 1/3)
   3.   ?    2
   4.   ?    1
   5.   ?    Ninguno de los anteriores