| En la Figura 4 hemos construido dos circunferencias
concéntricas. En la Figura 5 hemos elegido dos sectores generados por
ambas circunferencias y los dos radios. Y en la figura 6 hemos separado
ambos sectores circulares. Podemos verificar que si bien tienen la misma
forma no tienen el mismo tamaño. En primer lugar, las líneas azules (que
son los radios) son diferentes, en segundo lugar los arcos (de color rojo)
también son diferentes. Lo único que tienen en común es la "abertura"
formada por los dos radios. Y la razón es simple, si volvemos a superponer
ambos segmentos circulares de la Figura 6, volveremos a formar la Figura
5, esto es las líneas azules coincidirán que son las que acotan la
"abertura". Esta abertura los profesores de matemática le llaman
ángulo. |
| Cualquiera de los ángulos formados en la Figura 3, que la
forman dos rectas perpendiculares, se llama
ángulo recto. |
| Observemos entonces que la construcción de un ángulo es
independiente del radio de la circunferencia, y solo dependerá de las
direcciones que tomen ambas rectas (recuerde, siempre un ángulo será
formado por dos rectas). En rigor, dos rectas forman cuatro ángulos
siempre, de tal forma que los ángulos opuestos siempre serán iguales. Vea
la siguiente Figura Fundamental: |
|
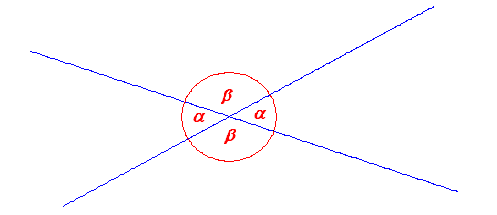
Figura Fundamental |
| Por una sana costumbre, los profesores de
matemática acostumbran a denotar los ángulos con letras griegas. En este
caso, a los ángulos iguales se les denota por la misma letra griega (a
se lee alfa, y b se lee beta). Podemos notar
que la suma de los ángulos a y
b forman el doble de un ángulo recto, que
llamaremos ángulo extendido. |
