Rectas perpendiculares

Ya hemos dicho que dos rectas en el plano son perpendiculares si entre ellas forman un ángulo recto (en rigor, se formen cuatro ángulos rectos). Por otro lado, aceptaremos como un axioma que por dos puntos distintos en el plano pasa una única recta, o de otra forma una recta está completamente determinada si conocemos de ella dos puntos distintos. Tenemos entonces que por un punto en el plano pueden pasar infinitas rectas. Sin embargo dada una recta determinada por dos puntos y tenemos otro punto que no pertenece a la recta, entonces por dicho punto pasa una única recta que es perpendicular a la primera. Veamos la situación en forma gráfica.

Por los puntos A y B trazamos la única recta que pasa por estos puntos, luego por el punto C, que no pertenece a dicha recta trazamos, la única recta perpendicular que se intercepta en el punto D. Se dice entonces que la recta AB es perpendicular a la recta CD y se escribe como

Supongamos ahora que elegimos un punto E distinto de D que pertenezca a la recta AB y trazamos la recta que pasa por C y E, como se observa en la siguiente figura:

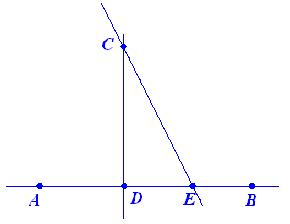
Entonces tenemos que el segmento de recta CD es mayor que el segmento de recta CE.

Si bien es cierto que el dibujo es evidencia este resultado, debemos hacer una demostración rigurosa con los conceptos que sabemos. Veamos como demostraremos que CD > CE. Si tomamos como centro el punto C y consideramos la circunferencia de radio igual a la longitud del segmento CD, tenemos que la recta AB es una recta tangente a dicha circunferencia siendo D el punto de tangencia que pertenece tanto ala recta como a la circunferencia, de modo que el punto E queda fuera de esa circunferencia, y por lo tanto la longitud del segmento CE es mayor que el radio CD. Y con esto queda demostrada la aseveración.

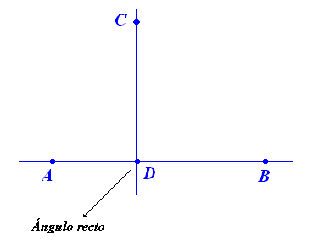
Con la misma figura anterior, habíamos dicho que por el punto C podemos trazar infinitas rectas, pero solo una va a ser perpendicular a la recta AB. Ahora bien, de todas las rectas que pasan por C, y que no sea la perpendicular a la recta AB, y cortan a la recta AB por un punto (que será distinto al punto D) se llaman rectas oblicuas a la recta AB. Sin embargo, hay una recta que pasa por C y que no corta jamás a la recta AB, tal recta se dice que es paralela a la recta AB. Vea la figura siguiente:

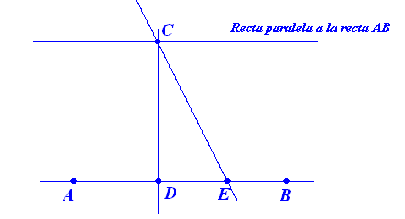¿Cómo caracterizamos a esta recta?, ¿qué propiedad tiene esta recta que la hace paralela a la recta AB?. Consideremos el punto B de la recta AB, y sobre este punto tracemos la única recta que pasa por B y que es perpendicular a la recta AB. Nos queda la siguiente figura

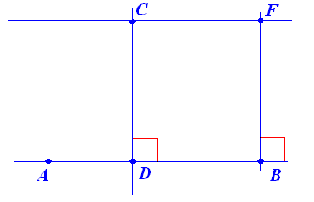Pues bien, la recta CF para que no se corte con la recta AB debe ocurrir que las distancias de los segmentos CD y FB sean iguales. De otra forma, dos rectas serán paralelas en el plano, si por todo punto de una de ellas se trazan las perpendiculares hacia la otra recta, todos los segmentos de rectas formadas entre estas dos rectas tienen la misma longitud. En rigor, para dos rectas paralelas, la distancia entre ellas es la longitud del segmento de recta generada por una perpendicular a ambas.

A propósito, la figura formada por los puntos DBFC es un rectángulo.

Rectas perpendiculares y paralelas