Circunferencia, círculo, cuerda, arco: definiciones formales

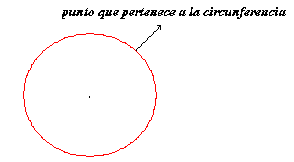
Ahora bien, el conjunto de puntos que se encuentran al interior de la circunferencia y los puntos de la misma circunferencia constituyen lo que se llama círculo.

Las dos figuras anteriores muestran la diferencia entre el concepto de circunferencia y círculo. De otra forma, el círculo está acotado por su circunferencia.

Diremos que dos circunferencias serán iguales si ambas tienen el mismo radio. (Nota para el profesor: Observe que es una definición contraproducente, puesto que si el alumno elige como centro dos puntos distintos y construye las circunferencia con el mismo radio, es obvio que "estos dos objetos" no serán "químicamente" iguales. Sin embargo podríamos optar por la palabra equivalentes. Esto es, dos circunferencias son equivalentes si ambas tienen el mismo radio)

Veamos algunos conceptos geométricos útiles para formalizar un lenguaje geométrico en torno a la circunferencia.

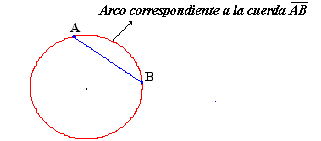
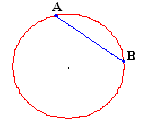
Si seleccionamos dos puntos A y B en la circunferencia, como lo indica la figura del frente, y por esos dos puntos trazamos el segmento de recta, al segmento, que llamaremos AB, lo denotaremos por cuerda AB. Observe que existe una cuerda muy especial, que es aquel segmento de recta que pasa por el centro y que ya habíamos visto que la longitud de esta cuerda constituye el diámetro. En particular la cuerda AB que hemos puesto como ejemplo aquí es claramente menor que el diámetro de la circunferencia.

Sobre el mismo dibujo anterior, los puntos A y B determinan dos porciones de circunferencia que llamaremos arcos. Y el arco menor lo llamaremos arco correspondiente a la cuerda AB. Es claro que nos encontraremos en problemas en elegir el arco correspondiente a un diámetro, puesto que un diámetro generará dos arcos de circunferencia iguales. En este caso no hay problemas de elegir indistintamente alguno de los dos arcos (que serán iguales en su longitud). Este hecho es muy importante, puesto que en estricto rigor el arco correspondiente a un diámetro forma una media circunferencia.

Observemos la rica pizza (aproximadamente) circular que hizo este cocinero. Es claro que este cocinero está cortando la pizza mediante una cuerda que no pasa por el centro de la pizza, ¿correcto?. El arco que sustenta el corte del cuchillo se encuentra a la izquierda de su pantalla. En rigor la superficie superior de esta pizza se puede tratar aproximadamente como un círculo. Y el borde de la pizza se puede considerar como la circunferencia. Notemos que si el cocinero hubiese pasado su cuchillo por el centro de la pizza hubiésemos obtenidos dos mitades iguales de la pizza. Observe que la longitud del arco que sustenta el corte del cuchillo (al lado izquierdo) es claramente menor a la longitud del arco que está a la derecha.

Ahora observemos este delicioso queso circular, al cual se le ha sacado un trozo. Observemos que quien cortó el queso, hizo dos cortes desde el centro de la circunferencia hacía afuera. ¿Cuánto queso aproximadamente falta? Los dos cortes fueron trazados aproximadamente "perpendiculares", de tal manera que aproximadamente fue extraído la cuarta parte del queso (ya sea la cuarta parte de su peso o de su volumen), de manera que el arco que falta también será igual a la cuarta parte del perímetro de la circunferencia. Esto de trazar segmentos de rectas desde el centro de una circunferencia hacía fuera es uno de los procedimientos más notables para el cálculo matemático. De hecho usted ya aprendió cuando dos rectas son perpendiculares: Dos rectas serán perpendiculares si, para cualquier circunferencia, estas dos rectas pasan por el centro de la circunferencia entonces dividen a la circunferencia en cuatro segmentos de arcos iguales.

En la próxima sesión veremos la relación que hay entre circunferencias, rectas y ángulos. No obstante antes necesitamos la idea de sector circular.

Observe el trozo de queso. Pues bien, el sector circular de una circunferencia está formado por dos radios y el arco que une los puntos de intersección de ambos radios con la circunferencia. En rigor se forman dos sectores circulares, pero entenderemos que el sector circular de interés será aquel que explícitamente se denota, como lo hacemos nosotros en la última figura y que está pintada de color lila.