Fenómenos de Espera

Eliseo Martínez H.

 

Introducción

Recuerdo que hace una decena de años un grupo de chicos de los últimos años de ingeniería me pedían ayuda para la modelación de procesos de transportes y carguíos. Se trataba de ciertos procesos estándares, pero no por clásicos exentos de complejidad, que involucraba líneas de espera, recorridos de un lugar de carguío a otro de descarga. Por lo general diseñábamos el algoritmo en la pizarra, según la característica del problema, discutíamos las funciones a utilizar para simular ciertos factores aleatorios, para posteriormente el alumno acudir a un lenguaje de programación y llevar a cabo el algoritmo de la modelación pertinente. Siempre me quedaba con una sensación de insatisfacción, puesto que no veíamos el modelo finalizado con los alumnos que me consultaban. Pues bien, han pasado largos 12 años desde esas consultas. Y en esos 12 años se ha sentido la tecnología, por lo menos algunos la hemos sentido en los procesos de modelación. En ese entonces nuestro problema en modelar era definitivamente que no identificábamos las variables de estado y las variables de flujo en los problemas de transporte y carguío. Ahora bastando la identificación y como interactúan las variables en el problema, la modelación se efectúa prácticamente dibujando la situación (en Chile diríamos haciendo el “monito”, el dibujito).

En honor a esos tiempos, y a esos alumnos que me consultaban, estableceré una serie de modelos que tratan con fenómenos de espera y transporte de la vida cotidiana utilizando la Dinámica de Sistemas y el software STELLA. Y habrá una finalidad doble. Aparte de enseñar los principios de la Dinámica de Sistemas, enseñaremos el uso del software STELLA en algunos aspectos poco frecuentes, hasta ahora, que tienen que ver con líneas de espera y submodelos.

 

Líneas de Espera en una Tienda

Supongamos la siguiente problemática. Se tiene una tienda mediana de autoservicio, de manera que los clientes deben entrar a la tienda, seleccionar la mercadería o artículos que desean y luego ir al área de las cajeras donde deben efectuar el pago, una vez realizado esto abandonan la tienda. Para la simplicidad del modelo existen ciertos supuestos que posteriormente pueden ser levantados o modificados. Existen clientes que se toman una hora en realizar la compra, así como una fracción importante de clientes que efectúan una compra rápida que les toma unos 15 minutos y van a hacia el sector de las cajas a pagar. La llegada de los clientes a la tienda se regula mediante un proceso de Poisson con parámetro que varían de acuerdo a la hora del día. Existen tres cajas en esta tienda, pero una tercera caja actúa solo en caso de emergencia; más preciso., la tercera caja solo se abre si existen más de 10 personas en total esperando pagar entre las otras dos cajas restantes.

 

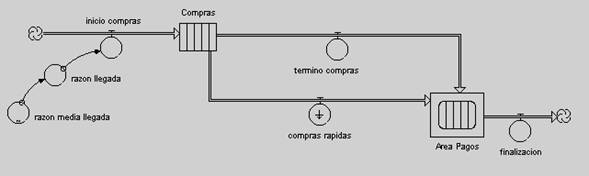
Figura 1

 

Identificaremos dos variables de estado para este problema. La primera, el número de personas que entran a elegir sus artículos que llamaremos Compras; y la segunda, la gente que entra a las líneas de espera a pagar en las cajas de la tienda, que llamaremos Area Pagos. La primera variable de estado , y es alimentada por una variable de flujo que llamaremos inicio compras, y ella nos entrega los clientes que llegan (o no llegan) a cada instante de tiempo a la tienda y será modelada por una distribución de Poisson que hemos llamado razón de llegada, y esta variable dependerá de un parámetro llamado razón media llegada que a su vez dependerá de la hora del día. Como sea, una vez que entra gente a la tienda, esta tardará un determinado tiempo en permanecer en esa variable de estado, ya sea si ocupa la hora en comprar o hace una compra rápida que le tome 15 minutos. La permanencia en la variable de estado Compras es similar a permanecer en una correa transportadora (conveyor, en inglés) que tardará una hora, excepto para la gente que realiza una fuga (leakage, en inglés) y que solo permanecerá en esa “correa transportadora” 15 minutos. En cualquier caso, tanto como los que permanecen una hora como los que permanecen 15 minutos, se dirigirán al sector de las cajas mediante sendos flujos (termina compra, compra rápida), y así ingresarán al sector Area Pagos. Aquí realizarán ciertas actividades como: mirar que línea de espera es la más corta y elegir ella, esperar en esa fila elegida para iniciar el pago a la persona que está en la caja, mientras que la persona que está en la caja tiene, en promedio, un tiempo de atención para cada cliente, y una vez que el éste realiza el pago se retira de la tienda. Por otro lado existe un supervisor que indicará cuando abrir una tercera caja en caso de que se produzca un colapso en las líneas de espera (colapso para el supervisor significa el nivel de 10 personas esperando pagar en las dos filas). Bien, todo este complicado proceso estará dentro de la caja negra (siempre se utiliza ese color cuando no se sabe que pasa en un proceso, propongo cambiarlo por caja blanca) que hemos llamado Area Pagos, y que en la figura 1 la hemos marcado con una notación especial que significa sub-modelo, es decir que allí (dentro de ella modelaremos el último párrafo marcado en cursiva). Una vez finalizado el proceso de pago las personas se retiran de la tienda mediante el flujo de salida finalización.

Pues bien, con todo lo anterior parece que el “monito” o esquema o dibujo indicado en la figura 1 resulta bastante claro. Vamos a ir entonces icono por icono para establecer las relaciones analíticas.

 

Poisson: Discretización y continuidad.

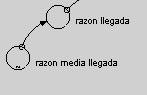
Figura 2

 

La distribución de Poisson, conocida también acertadamente como la ley de los raros eventos, es una distribución para eventos discretos. En rigor, si decimos que una variable aleatoria discreta X se distribuye según una Poisson de parámetro , estamos diciendo que

 

 

De manera que si aseguramos que las llegadas de los clientes al supermercado se distribuye según una Poisson con parámetro = razón media llegada, como se ve en la figura 2, estamos entonces simulando la llegada de clientes a la tienda mediante la variable razón de llegada. La programación de esta última variable es en extremo sencilla, y basta con la instrucción

Razon llegada = POISSON (razon media llegada, 123)

 

(nota: ex profeso no he puesto acento en “razon”, por la sencilla razón de que el software STELLA no acepta los acentos). El valor de 123 en la instrucción anterior significa establecer una “semilla”, de tal forma que para cualquier repetición de la simulación se obtengan los mismos números aleatorios que se obtuvieron la primera vez al echar a correr el programa.

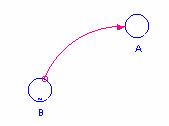
Habíamos dicho que la razón media de llegada es función de las horas del día, de modo que estableceremos la variable “razon media llegada” como función de las 24 horas del día, y esto se hace de la siguiente forma (vamos a enseñar el procedimiento para hacer una tabla o gráfico de una variable B, y luego que la variable A dependa de B, esto es A = f(B). En primer lugar dibujar A y B, como variables simples, luego trazar un conector desde B hacia A, como lo indica la figura 3.

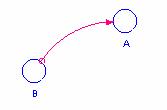
Figura 3

 

Ahora, haciendo doble clic en la variable B, vamos a trazar una tabla de modo que B tenga valores que dependan del tiempo como lo indica la tabla 1.

 

Tabla 1

 

Donde la primera columna indica el tiempo en horas de un día determinado y la otra columna denota los parámetros correspondiente a una distribución de Poisson. Es decir, por ejemplo, para la hora cero el parámetro vale 6, en la hora 2 el parámetro vale 8, y así sucesivamente.  Ahora bien, en primer lugar vamos a enseñar como hacer esta tabla en la variable B de nuestro modelo. Haciendo doble clic en la variable B, aparecerá la siguiente caja de diálogo de la figura 4:

 

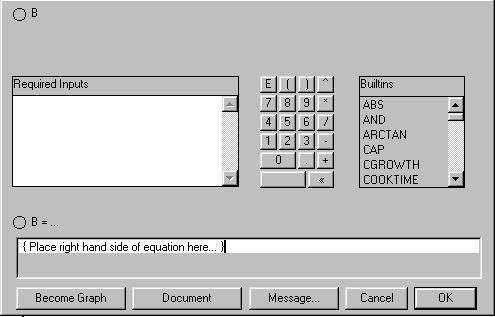
Figura 4

 

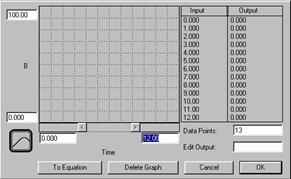
Puesto que a la variable B la haremos depender del tiempo (TIME, en el lenguaje de STELLA), entonces en el lugar de “Place right han side of equation here...” ponemos la expresión TIME (figura 5), y luego oprimimos la tecla “Become Graph” (figura 6).

 

Figura 5

Figura 6

 

Si observamos la figura 6, por defecto aparece una partición de 13 puntos, donde el eje X asume el rango entre 0 y 12, y el eje Y el rango entre 0 y 100. Observando nuestra tabla 1, vemos que el rango de las X (TIME) está entre 0 y 24, con 13 puntos, y el rango de los parámetros es de 6 a 25 (digamos entre 0 y 30, para dar margen a futuras variaciones). De modo que lo que realizaremos es redefinir los valores en los ejes X e Y (y aceptar los 13 puntos por defecto). La caja de diálogo debe lucir como en la figura 7.

 

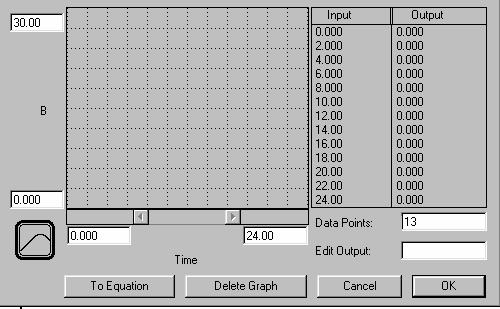
Figura 7

 

Ahora posicionamos el cursor en la columna “Output”, lo cual hará activar la caja “Edit Output” y allí escribimos el valor que corresponda al valor de la columna “Input” según la tabla 1. Se indica en la figura 8 en proceso hasta el valor 10.

 

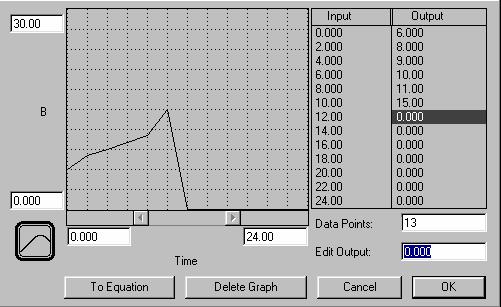
Figura 8

 

Una vez completada esta tabla oprimimos la tecla OK, y deberá aparecer el icono indicada en la figura 9.

Figura 9

 

Nuestro interés ahora es que la variable A sea una función de B, y más aún que B sea un generador de números aleatorios obtenidas de una distribución de Poisson con parámetro dado por la función B. Para esto hacemos doble clic en la variable A y seleccionamos de la caja de diálogos “Builtins” la función POISSON y ponemos en su argumento el parámetro representado por la letra B como lo indica la figura 10.

 

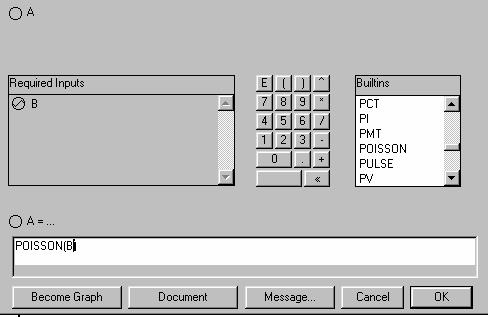
Figura 10

 

Ahora bien, vamos a ver como opera esta función, la de Poisson, en función del tiempo.

 

Tiempo discreto y tiempo continuo.

 Cuando en modelación se habla de tiempo discreto significa que la variable tiempo (TIME) tome valores sobre un conjunto discreto, en particular en  (aunque este no es el caso general). De manera que podemos fijar la variación del tiempo TIME como

 

TIME =

Con  y , de manera que la iteración de la variable TIME recorrerá todos los valores de 0, 1, 2, ... hasta un valor determinado N.

Si entendemos así el tiempo discreto, es decir igualmente espaciados con incremento igual a la unidad, podemos hacer simulación discreta. Vamos entonces a hacer una iteración del modelo recién construido con el diagrama indicado en la figura 11 con el valor de sus relaciones indicada en la tabla 2.

 

Figura 11

Tabla 2

 

Para hacer una iteración vamos a elegir un tiempo discreto que vaya desde 0 hasta 24 con incrementos igual a la unidad, para esto seleccionamos la opción “RUN”, y luego “Time Specs”, y en la caja de diálogo que aparecerá escribimos lo anteriormente indicado. Ver la figura 12.

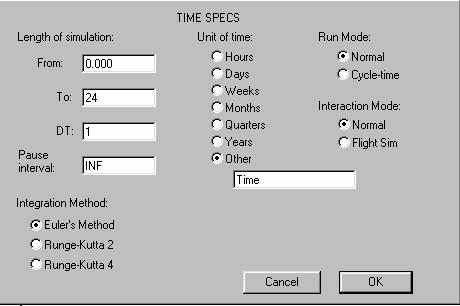
Figura 12

 

Aceptamos esta longitud de simulación oprimiendo OK, luego sacamos una tabla de valores para ver los valores obtenidos para la variable A, y al elegir la opción RUN aparecerán los valores indicados en la tabla 3 (si usted realiza este ejercicio, lo más probable que obtenga otros valores levemente diferentes, recuerde que está generando valores aleatorios según una Poisson).

 

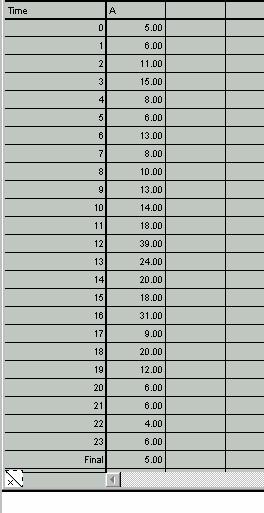
Tabla 3

 

¿Qué significan estos valores? Significa sencillamente que, por ejemplo en la iteración 20 el software ha generado un número aleatorio, el número 6, que proviene de una Poisson con el parámetro indicado para el tiempo (la hora) 20, esto es de parámetro 10. Otro ejemplo, en la iteración 2 se ha generado el número 11 que proviene de una distribución de Poisson de parámetro 8. (Los parámetros en relación al tiempo se obtienen de la tabla 1).

 

Ahora bien, vamos a suponer que la función A en nuestro modelo de la figura 11 representa la llegada de clientes a una tienda, y estos clientes llegan durante el día, es decir la llegada es a cualquier instante del intervalo [0,24]. Si es este el caso se dice que el tiempo es una variable continua. Es decir a las 11 horas con 37 minutos y 11 segundos pueden llegar, por ejemplo, 3 clientes a la tienda. ¿Cómo podemos realizar este experimento aleatorio en nuestro modelo dela figura 11?

Para esto, siempre con abuso de lenguaje, hacemos una partición más fina de nuestra longitud de simulación, de modo que interprete de forma aproximada situaciones como “ a las 11 horas con 37 minutos y 11 segundos”, que puede ser una partición del tipo

 

TIME =

Con (nota importante, el incremento debe ser divisor exacto de la unidad, en este caso la división es 32). Realizando estos cambios como lo indica la figura 13, realizamos una simulación que aparecerá (una parte de ella) en la tabla 4, donde esta vez incluiremos los valores de B.

 

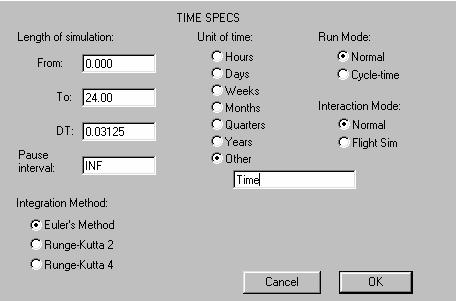
Figura 13

 

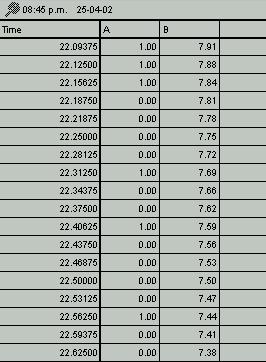
Tabla 4

 

¿Qué ha sucedido? ¿Porqué los valores son tan diferentes a los entregados en la tabla 3?

Lo que ha ocurrido es que esta vez la generación de los números aleatorios ha utilizado como parámetro para la de Poisson el valor de B*. Por ejemplo el número generado en la iteración correspondiente al tiempo 22.31250, que es el número 1, ha sido obtenido de una distribución de Poisson de parámetro correspondiente a la interpolación simple entre 22 y 23 correspondiente al punto 22.31250, que es 7.69, multiplicado por , es decir se ha obtenido el número aleatorio 1 según una Poisson de parámetro 7.60*0.03125 = 0.2403125.

De otra forma, cuando se hace el proceso discreto con valores espaciados en intervalos de 1 hora, como el contenido en la tabla 3, al hacer la partición más fina (tratando de hacerla continua), el software STELLA intenta predecir a las personas que llegan en los instantes que componen una hora determinada. Es decir, se concluye, mirando la tabla 4 que entre las 22.09375 horas y las 22.09375 horas llegaron 6 personas (la suma de los unos generados).

 

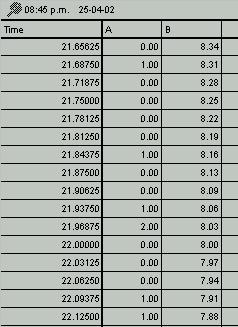
Tabla 5

 

La tabla 5 nos entrega otro segmento de simulación, donde se puede concluir que entre las 21.65625 y 22.12500 horas llegaron 7 personas, y que (en esta simulación) a las 21.96875 hora (casi a las 10 de la noche) llegaron 2 personas a la tienda.

Para finalizar con el icono de la figura 2, que es el motivo de esta sección, simplemente reemplazamos en nuestro modelo de la figura 3, la variable A por razon llegada (sin acento) y B por razon media llegada (también sin acento).

 

26 de abril del 2002