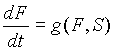
Eliseo Martínez H.
F : número de peces de una cierta especie (que son alimentos de los tiburones)
S: número de tiburones en la misma área que habitan los peces.
El área se supone acotada de tal manera que si el cruce migratorio no es posible, al menos no tenga ningún efecto mayor. Otras suposiciones se harán para establecer el modelo diferencial
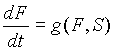
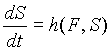
Antes de formular un modelo específico, trataremos de describir los efectos deseados para este modelo. Si los pescadores se abstienen de pescar a los peces (que se alimentan de plancton) por un par de años entonces se debiera esperar que esta población de peces crezca en tamaño. Una vez que haya crecido, los tiburones deberían tener suficiente alimento para sostener una gran población de escualos. Entonces la población de escualos debería aumentar, y en un tiempo corto plantear un severo trato a los peces. Eventualmente la población de peces debería disminuir. Una vez que la población de peces haya disminuido en número, los tiburones no podrán sostener su gran población y deberá disminuir su población. Esto permitirá a su vez que la población de peces vuelva al tamaño de la población original. Es posible que este proceso continúe indefinidamente, en cuyo caso el ecosistema consistirá en una población de variación periódica.
Esta descripción de la interacción de peces y tiburones se puede aplicar a otras situaciones de depredador-presa. Entonces el modelo a desarrollar aquí puede tener validez para otros ecosistemas basados en las consideraciones que relacionan a los peces y tiburones. Para otro ejemplo de interacción entre dos especies, considere la población de linces y liebres en Canadá. Observaciones de estas poblaciones han sido accesibles por muchos años. Los tramperos de la Hudson Bay Company, que cazaban ambas especies, los linces y las liebres, mantenían buenos registros de los números de linces y liebres cazadas (presumiblemente reflejando a las poblaciones totales de linces y liebres). Los datos revelan notables fluctuaciones periódicas de ambas poblaciones como se indica aquí.
En el desarrollo de un modelo de un ecosistema representando la interacción de dos especies, es ventajoso primero modelar el crecimiento poblacional ignorando las interacciones entre las especies. Entonces nos preguntaremos, ¿qué ecuaciones debería satisfacer los tiburones si no estuviesen los peces?, y viceversa.
Al considerar los peces sin los tiburones, las suposiciones concernientes a los procesos de nacimiento y muerte de los peces debe ser delineada. Puesto que los peces comen plancton, que se supone en abundancia, parece natural que la razón de crecimiento de los peces (sin tiburones) es constante,
.
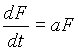la razón de nacimiento es más grande que la razón de muerte, produciendo un crecimiento exponencial. Esto supone que el plancton es ilimitado. Por otro lado, si el crecimiento de la población de peces cesa hasta un tamaño determinado, entonces se puede proponer un modelo logístico de crecimiento de la forma,
.
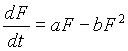Entonces la razón de cambio de los peces, 
, es tal que 
está dada por 
o por 
. Esta última ecuación incorpora a la primera. Si 
, entonces existe una población de peces en equilibrio, digamos 
, si no existen tiburones.
Los tiburones se comportan manera diferente. Si no hay peces, entonces la fuente de alimento no existe. En este caso, la razón de muerte de los tiburones es razonable que exceda a la razón de nacimiento. Luego en ausencia de peces se supone que
.
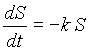Sin peces, los tiburones deberían eventualmente a desaparecer. Entonces hemos
determinado que 
, donde 
.
Ahora modelaremos la interacción compleja entre los peces y los tiburones. La
existencia de peces aumenta la población de tiburones; entonces los peces causarán un
aumento en la razón de crecimiento de los tiburones. Para la simplicidad en el modelo
matemático de este proceso, supondremos que la razón de crecimiento de tiburones está
aumentando proporcionalmente al número de peces. La razón de crecimiento de los
tiburones, que era de 
sin peces, es
modelada ahora como 
con peces, donde 
es la constante de proporcionalidad positiva.
Entonces
.
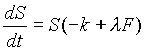Para modelar el desarrollo de los peces, usaremos ideas similares. Sin embargo, en este
caso la existencia de tiburones hará disminuir la razón de crecimiento de los peces.
Supondremos nuevamente que el efecto de interacción sobre la razón de crecimiento es
proporcional a la población. Consecuentemente la razón de crecimiento de los peces, que
fue de 
sin tiburones, llegará a ser de 
con tiburones, donde 
es la constante de proporcionalidad positiva. Entonces hemos
descrito el trasfondo para el conjunto de ecuaciones diferenciales desarrolladas
independientemente por Lotka y Volterra
en la década de 1920,
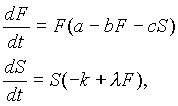
donde las constantes 
que describen el
proceso son todas positivas (excepto para 
que
puede ser 0 sí una cantidad ilimitada de plancton existe en la zona). Este no es el
único modelo posible de un ecosistema depredador y presa, pero es uno de los más
simples.
A continuación presentamos el Diagrama de Forrester del modelo:
